In or Out?
I've been stalling, trying not to say too much about spatial until it's actually available. The code has all been in for some time now, but its been waiting for its release vehicle: the next CTP. Hopefully it should be in your hands in a few weeks.
Of course, if you've been following spatial closely, you may have noticed that there seem to be a few folks who have the code already, and they're generating a little noise, so maybe I ought not be so quiet.
The latest post I've seen is from Roger Doherty here at MS. To selectively snip from Roger's much longer post:
One interesting thing I ran into when creating the geography polygons was that you have to define the polygon's points in a counter-clockwise fashion to have the proper "ring orientation". If you define geography points in a clockwise fashion you will get the following error:
...
I don't confess to understand this 100%, but Ed Katibah told me its kind of like turning the world inside-out. Ed also mentioned that sister data type geometry polygons don't have this limitation and can be loaded in either order (clockwise or counter-clockwise).
I discussed this briefly in an earlier post, but let me say a bit more here. The new geometry type works on the plane. A polygon on the plane is well-defined, regardless of orientation. I.e., these two loops define the same region:
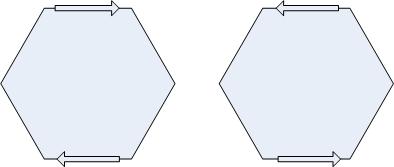
To explain, we have to look at how we determine whether a point is inside and outside of the polygon. Conceptually, what we do is project a ray from the point to infinity, and ask how many times the ray crosses the figure: odd count means the point is in, even means it's out. This works because we can define any point at infinity to be outside the polygon, and every time we cross the boundary we flip from inside to outside. Here, the ray from the top point crosses a boundary four times, so the point is outside the figure; the ray for the bottom point only crosses thrice, so it's in.
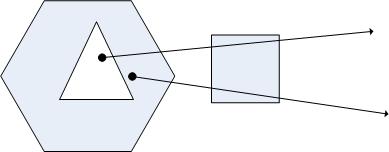
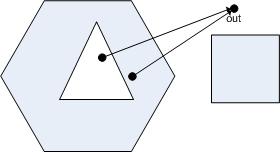
You'll notice that this definition doesn't rely on the orientation of the rings at all. Also, if we were to simply define a particular point to be outside the polygon, we wouldn't need to draw rays to infinity. E.g., this works equally well, assuming we knew that "out" was out:
Now, let's consider what happens if we work on the sphere (or an ellipsoid) instead of the plane as we do with the geography. Unlike the plane, the sphere is bounded, so we can't conceptually project a ray to infinity and count crossings. If we could pick a point that was outside of all polygons, then we could count crossings on a path to that point, but we can't do that either. To make this concrete, what would happen if we were to define a polygon by drawing a ring around the equator: would the northern or southern hemisphere be in?
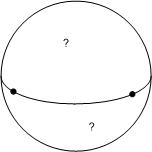
We can rectify the situation, but to do so we have to enforce an edge direction scheme. In our case, we simply add the definition that if you were to walk along the edge of a polygon, the inside will always be to your left. If you invert the order of your edges, you swap the interior for the exterior---you "turn the world inside-out". Visually:
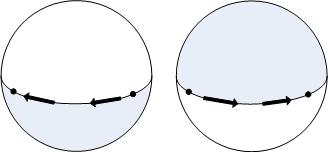
Now, it turns out that we're also pretty lax about accepting polygons in the geometry type. If we're handed a set of rings that overlap each other, we can still figure out what they mean, for example. (The OGC doesn't like these, and we won't let you do much with them, but we will ingest them and let you turn them into an equivalent OGC-valid set of polygon or multipolygon.) It turns out that we have to be much pickier about these when we go to round-earth computations as well, since they can very easily become ill-defined.
Cheers,
-Isaac