OpenType™ Layout Common Table Formats (OpenType 1.5)
OpenType Layout consists of five tables: the Glyph Substitution table (GSUB), the Glyph Positioning table (GPOS), the Baseline table (BASE), the Justification table (JSTF), and the Glyph Definition table (GDEF). These tables use some of the same data formats.
This chapter explains the conventions used in all OpenType Layout tables, and it describes the common table formats. Separate chapters provide complete details about the GSUB, GPOS, BASE, JSTF, and GDEF tables.
Overview
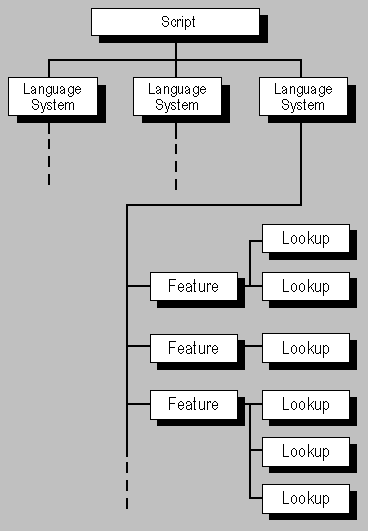
The OpenType Layout tables provide typographic information for properly positioning and substituting glyphs, operations that are required for accurate typography in many language environments. OpenType Layout data is organized by script, language system, typographic feature, and lookup. Scripts are defined at the top level. A script is a collection of glyphs used to represent one or more languages in written form (see Figure 2a). For instance, a single script-Latin-is used to write English, French, German, and many other languages. In contrast, three scripts-Hiragana, Katakana, and Kanji-are used to write Japanese. With OpenType Layout, multiple scripts may be supported by a single font.

A language system may modify the functions or appearance of glyphs in a script to represent a particular language. For example, the eszet ligature is used in the German language system, but not in French or English (see Figure 2b). And the Arabic script contains different glyphs for writing the Farsi and Urdu languages. In OpenType Layout, language systems are defined within scripts.
A language system defines features, which are typographic rules for using glyphs to represent a language. Sample features are a "vert" feature that substitutes vertical glyphs in Japanese, a "liga" feature for using ligatures in place of separate glyphs, and a "mark" feature that positions diacritical marks with respect to base glyphs in Arabic (see Figure 2c). In the absence of language-specific rules, default language system features apply to the entire script. For instance, a default language system feature for the Arabic script substitutes initial, medial, and final glyph forms based on a glyph’s position in a word.
Features are implemented with lookup data that the text-processing client uses to substitute and position glyphs. Lookups describe the glyphs affected by an operation, the type of operation to be applied to these glyphs, and the resulting glyph output.
Table Organization
Two OpenType Layout tables, GSUB and GPOS, use the same data formats to describe the typographic functions of glyphs and the languages and scripts that they support: a ScriptList table, a FeatureList table, and a LookupList table. In GSUB, the tables define glyph substitution data. In GPOS, they define glyph positioning data. This chapter describes these common table formats.
The ScriptList identifies the scripts in a font, each of which is represented by a Script table that contains script and language-system data. Language system tables reference features, which are defined in the FeatureList. Each feature table references the lookup data defined in the LookupList that describes how, when, and where to implement the feature.
Note: The data in the BASE and JSTF tables also is organized by script and language system. However, the data formats differ from those in GSUB and GPOS, and they do not include a FeatureList or LookupList. The BASE and JSTF data formats are described in the BASE and JSTF chapters.
The information used to substitute and position glyphs is defined in Lookup subtables. Each subtable supplies one type of information, depending upon whether the lookup is part of a GSUB or GPOS table. For instance, a GSUB lookup might specify the glyphs to be substituted and the context in which a substitution occurs, and a GPOS lookup might specify glyph position adjustments for kerning. OpenType Layout has seven types of GSUB lookups (described in the GSUB chapter) and nine types of GPOS lookups (described in the GPOS chapter).
Each subtable (except for an Extension LookupType subtable) includes a Coverage table that lists the "covered" glyphs that will result in a glyph substitution or positioning operation. The Coverage table formats are described in this chapter.
Some substitution or positioning operations may apply to groups, or classes, of glyphs. GSUB and GPOS Lookup subtables use the Class Definition table to assign glyphs to classes. This chapter includes a description of the Class Definition table formats.
Lookup subtables also may contain device tables, described in this chapter, to adjust scaled contour glyph coordinates for particular output sizes and resolutions. This chapter also describes the data types used in OpenType Layout. Sample tables and lists that illustrate the common data formats are supplied at the end of this chapter.
Scripts and Languages
Three tables and their associated records apply to scripts and languages: the Script List table (ScriptList) and its script record (ScriptRecord), the Script table and its language system record (LangSysRecord), and the Language System table (LangSys).
Script List Table and Script Record
OpenType Layout fonts may contain one or more groups of glyphs used to render various scripts, which are enumerated in a ScriptList table. Both the GSUB and GPOS tables define Script List tables (ScriptList):
- The GSUB table uses the ScriptList table to access the glyph substitution features that apply to a script. For details, see the chapter, The Glyph Substitution Table (GSUB).
- The GPOS table uses the ScriptList table to access the glyph positioning features that apply to a script. For details, see the chapter, The Glyph Positioning Table (GPOS).
A ScriptList table consists of a count of the scripts represented by the glyphs in the font (ScriptCount) and an array of records (ScriptRecord), one for each script for which the font defines script-specific features (a script without script-specific features does not need a ScriptRecord).
If a Script table with the script tag 'DFLT' (default) is present in the ScriptList table, it must have a non-NULL DefaultLangSys and LangSysCount must be equal to 0. The 'DFLT' Script table should be used if there is not an explicit entry for the script being formatted.
The ScriptRecord array stores the records alphabetically by a ScriptTag that identifies the script. Each ScriptRecord consists of a ScriptTag and an offset to a Script table.
Example 1 at the end of this chapter shows a ScriptList table and ScriptRecords for a Japanese font that uses three scripts.
ScriptList table
| Type | Name | Description |
|---|---|---|
| uint16 | ScriptCount | Number of ScriptRecords |
| struct | ScriptRecord[ScriptCount] | Array of ScriptRecords -listed alphabetically by ScriptTag |
ScriptRecord
| Type | Name | Description |
|---|---|---|
| Tag | ScriptTag | 4-byte ScriptTag identifier |
| Offset | Script | Offset to Script table-from beginning of ScriptList |
Script Table and Language System Record
A Script table identifies each language system that defines how to use the glyphs in a script for a particular language. It also references a default language system that defines how to use the script’s glyphs in the absence of language-specific knowledge.
A Script table begins with an offset to the Default Language System table (DefaultLangSys), which defines the set of features that regulate the default behavior of the script. Next, Language System Count (LangSysCount) defines the number of language systems (excluding the DefaultLangSys) that use the script. In addition, an array of Language System Records (LangSysRecord) defines each language system (excluding the default) with an identification tag (LangSysTag) and an offset to a Language System table (LangSys). The LangSysRecord array stores the records alphabetically by LangSysTag.
If no language-specific script behavior is defined, the LangSysCount is set to zero (0), and no LangSysRecords are allocated.
Script table
| Type | Name | Description |
|---|---|---|
| Offset | DefaultLangSys | Offset to DefaultLangSys table-from beginning of Script table-may be NULL |
| uint16 | LangSysCount | Number of LangSysRecords for this script-excluding the DefaultLangSys |
| struct | LangSysRecord [LangSysCount] |
Array of LangSysRecords-listed alphabetically by LangSysTag |
LangSysRecord
| Type | Name | Description |
|---|---|---|
| Tag | LangSysTag | 4-byte LangSysTag identifier |
| Offset | LangSys | Offset to LangSys table-from beginning of Script table |
Language System Table
The Language System table (LangSys) identifies language-system features used to render the glyphs in a script. (The LookupOrder offset is reserved for future use.)
Optionally, a LangSys table may define a Required Feature Index (ReqFeatureIndex) to specify one feature as required within the context of a particular language system. For example, in the Cyrillic script, the Serbian language system always renders certain glyphs differently than the Russian language system.
Only one feature index value can be tagged as the ReqFeatureIndex. This is not a functional limitation, however, because the feature and lookup definitions in OpenType Layout are structured so that one feature table can reference many glyph substitution and positioning lookups. When no required features are defined, then the ReqFeatureIndex is set to 0xFFFF.
All other features are optional. For each optional feature, a zero-based index value references a record (FeatureRecord) in the FeatureRecord array, which is stored in a Feature List table (FeatureList). The feature indices themselves (excluding the ReqFeatureIndex) are stored in arbitrary order in the FeatureIndex array. The FeatureCount specifies the total number of features listed in the FeatureIndex array.
Features are specified in full in the FeatureList table, FeatureRecord, and Feature table, which are described later in this chapter. Example 2 at the end of this chapter shows a Script table, LangSysRecord, and LangSys table used for contextual positioning in the Arabic script.
LangSys table
| Type | Name | Description |
|---|---|---|
| Offset | LookupOrder | = NULL (reserved for an offset to a reordering table) |
| uint16 | ReqFeatureIndex | Index of a feature required for this language system- if no required features = 0xFFFF |
| uint16 | FeatureCount | Number of FeatureIndex values for this language system-excludes the required feature |
| uint16 | FeatureIndex[FeatureCount] | Array of indices into the FeatureList-in arbitrary order |
Features and Lookups
Features define the functionality of an OpenType Layout font and they are named to convey meaning to the text-processing client. Consider a feature named "liga" to create ligatures. Because of its name, the client knows what the feature does and can decide whether to apply it. For more information, see the "OpenType Layout Registered Features" chapter. Font developers can use these features, as well as create their own.
After choosing which features to use, the client assembles all lookups from the selected features. Multiple lookups may be needed to define the data required for different substitution and positioning actions, as well as to control the sequencing and effects of those actions.
To implement features, a client applies the lookups in the order the lookup definitions occur in the LookupList. As a result, within the GSUB or GPOS table, lookups from several different features may be interleaved during text processing. A lookup is finished when the client locates a target glyph or glyph context and performs a substitution (if specified) or a positioning (if specified).
Note: The substitution (GSUB) lookups always occur before the positioning (GPOS) lookups. The lookup sequencing mechanism in TrueType relies on the font to determine the proper order of text-processing operations.
Lookup data is defined in one or more subtables that contain information about specific glyphs and the operations to be performed on them. Each type of lookup has one or more corresponding subtable definitions. The choice of a subtable format depends upon two factors: the precise content of the information being applied to an operation, and the required storage efficiency. (For complete definitions of all lookup types and subtables, see the the GSUB and GPOS chapters of this document.)
OpenType Layout features define information that is specific to the layout of the glyphs in a font. They do not encode information that is constant within the conventions of a particular language or the typography of a particular script. Information that would be replicated across all fonts in a given language belongs in the text-processing application for that language, not in the fonts.
Feature List Table
The headers of the GSUB and GPOS tables contain offsets to Feature List tables (FeatureList) that enumerate all the features in a font. Features in a particular FeatureList are not limited to any single script. A FeatureList contains the entire list of either the GSUB or GPOS features that are used to render the glyphs in all the scripts in the font.
The FeatureList table enumerates features in an array of records (FeatureRecord) and specifies the total number of features (FeatureCount). Every feature must have a FeatureRecord, which consists of a FeatureTag that identifies the feature and an offset to a Feature table (described next). The FeatureRecord array is arranged alphabetically by FeatureTag names.
Note: The values stored in the FeatureIndex array of a LangSys table are used to locate records in the FeatureRecord array of a FeatureList table.
FeatureList table
| Type | Name | Description |
|---|---|---|
| uint16 | FeatureCount | Number of FeatureRecords in this table |
| struct | FeatureRecord[FeatureCount] | Array of FeatureRecords-zero-based (first feature has FeatureIndex = 0)-listed alphabetically by FeatureTag |
FeatureRecord
| Type | Name | Description |
|---|---|---|
| Tag | FeatureTag | 4-byte feature identification tag |
| Offset | Feature | Offset to Feature table-from beginning of FeatureList |
Feature Table
A Feature table defines a feature with one or more lookups. The client uses the lookups to substitute or position glyphs.
Feature tables defined within the GSUB table contain references to glyph substitution lookups, and feature tables defined within the GPOS table contain references to glyph positioning lookups. If a text-processing operation requires both glyph substitution and positioning, then both the GSUB and GPOS tables must each define a Feature table, and the tables must use the same FeatureTags.
A Feature table consists of an offset to a Feature Parameters (FeatureParams) table (if one has been defined for this feature - see note in the following paragraph), a count of the lookups listed for the feature (LookupCount), and an arbitrarily ordered array of indices into a LookupList (LookupListIndex). The LookupList indices are references into an array of offsets to Lookup tables.
The format of the Feature Parameters table is specific to a particular feature, and must be specified in the feature’s entry in the Feature Tags section of the OpenType Layout Tag Registry. The length of the Feature Parameters table must be implicitly or explicitly specified in the Feature Parameters table itself. The FeatureParams field in the Feature Table records the offset relative to the beginning of the Feature Table. If a Feature Parameters table is not needed, the FeatureParams field must be set to NULL.
To identify the features in a GSUB or GPOS table, a text-processing client reads the FeatureTag of each FeatureRecord referenced in a given LangSys table. Then the client selects the features it wants to implement and uses the LookupList to retrieve the Lookup indices of the chosen features. Next, the client arranges the indices in the LookupList order. Finally, the client applies the lookup data to substitute or position glyphs.
Example 3 at the end of this chapter shows the FeatureList and Feature tables used to substitute ligatures in two languages.
Feature table
| Type | Name | Description |
|---|---|---|
| Offset | FeatureParams | = NULL (reserved for offset to FeatureParams) |
| uint16 | LookupCount | Number of LookupList indices for this feature |
| uint16 | LookupListIndex[LookupCount] | Array of LookupList indices for this feature -zero-based (first lookup is LookupListIndex = 0) |
Lookup List Table
The headers of the GSUB and GPOS tables contain offsets to Lookup List tables (LookupList) for glyph substitution (GSUB table) and glyph positioning (GPOS table). The LookupList table contains an array of offsets to Lookup tables (Lookup). The font developer defines the Lookup sequence in the Lookup array to control the order in which a text-processing client applies lookup data to glyph substitution and positioning operations. LookupCount specifies the total number of Lookup table offsets in the array.
Example 4 at the end of this chapter shows three ligature lookups in the LookupList table.
LookupList table
| Type | Name | Description |
|---|---|---|
| uint16 | LookupCount | Number of lookups in this table |
| Offset | Lookup[LookupCount] | Array of offsets to Lookup tables-from beginning of LookupList -zero based (first lookup is Lookup index = 0) |
Lookup Table
A Lookup table (Lookup) defines the specific conditions, type, and results of a substitution or positioning action that is used to implement a feature. For example, a substitution operation requires a list of target glyph indices to be replaced, a list of replacement glyph indices, and a description of the type of substitution action.
Each Lookup table may contain only one type of information (LookupType), determined by whether the lookup is part of a GSUB or GPOS table. GSUB supports five LookupTypes, and GPOS supports seven LookupTypes (for details about LookupTypes, see the GSUB and GPOS chapters of the document). Each LookupType is defined with one or more subtables, and each subtable definition provides a different representation format. The format is determined by the content of the information required for an operation and by required storage efficiency. When glyph information is best presented in more than one format, a single lookup may contain more than one subtable, as long as all the subtables are the same LookupType. For example, within a given lookup, a glyph index array format may best represent one set of target glyphs, whereas a glyph index range format may be better for another set of target glyphs.
During text processing, a client applies a lookup to each glyph in the string before moving to the next lookup. A lookup is finished for a glyph after the client makes the substitution/positioning operation. To move to the “next” glyph, the client will typically skip all the glyphs that participated in the lookup operation: glyphs that were substituted/positioned as well as any other glyphs that formed a context for the operation. However, in the case of pair positioning operations (i.e., kerning), the “next” glyph in a sequence may be the second glyph of the positioned pair (see pair positioning lookup for details).
A Lookup table contains a LookupType, specified as an integer, that defines the type of information stored in the lookup. The LookupFlag specifies lookup qualifiers that assist a text-processing client in substituting or positioning glyphs. The SubTableCount specifies the total number of SubTables. The SubTable array specifies offsets, measured from the beginning of the Lookup table, to each SubTable enumerated in the SubTable array.
Lookup table
| Type | Name | Description |
|---|---|---|
| uint16 | LookupType | Different enumerations for GSUB and GPOS |
| uint16 | LookupFlag | Lookup qualifiers |
| uint16 | SubTableCount | Number of SubTables for this lookup |
| Offset | SubTable [SubTableCount] |
Array of offsets to SubTables-from beginning of Lookup table |
Each of the first four bits can be set in order to specify additional instructions for applying a lookup to a glyph string. The LookUpFlag bit enumeration table provides details about the use of these bits.
The high byte is set to specify the type of mark attachment.
LookupFlag bit enumeration
| Type | Name | Description |
|---|---|---|
| 0x0001 | RightToLeft | This bit relates only to the correct processing of the cursive attachment lookup type (GPOS lookup type 3). When this bit is set, the last glyph in a given sequence to which the cursive attachment lookup is applied, will be positioned on the baseline.
Note: Setting of this bit is not intended to be used by operating systems or applications to determine text direction. |
| 0x0002 | IgnoreBaseGlyphs | If set, skips over base glyphs |
| 0x0004 | IgnoreLigatures | If set, skips over ligatures |
| 0x0008 | IgnoreMarks | If set, skips over combining marks |
| 0x00F0 | Reserved | For future use |
| 0xFF00 | MarkAttachmentType | If not zero, skips over all marks of attachment type different from specified. |
For example, in Arabic text, a character string might have the pattern <base character - mark character - base character>. That string could be converted into a ligature composed of two components, one for each base character, with the combining mark glyph over the first component. To produce this ligature, the font developer would set the IgnoreMarks bit to tell the client to ignore the mark, substitute the ligature glyph first, and then position the mark glyph over the ligature. Alternatively, a lookup which did not set the IgnoreMarks bit could be used to describe a three-component ligature glyph, composed of the first base glyph, the mark glyph, and the second base glyph. Here’s another example: A lookup which creates a ligature of a base glyph with a top mark may skip over all bottom marks by specifying the mark attachment type as top marks. You can define attachment types of marks in the MarkAttachClassDef subtable in the GDEF table.
Coverage Table
Each subtable (except an Extension LookupType subtable) in a lookup references a Coverage table (Coverage), which specifies all the glyphs affected by a substitution or positioning operation described in the subtable. The GSUB, GPOS, and GDEF tables rely on this notion of coverage. If a glyph does not appear in a Coverage table, the client can skip that subtable and move immediately to the next subtable.
A Coverage table identifies glyphs by glyph indices (GlyphIDs) either of two ways:
- As a list of individual glyph indices in the glyph set.
- As ranges of consecutive indices. The range format gives a number of start-glyph and end-glyph index pairs to denote the consecutive glyphs covered by the table.
In a Coverage table, a format code (CoverageFormat) specifies the format as an integer: 1 = lists, and 2 = ranges.
A Coverage table defines a unique index value (Coverage Index) for each covered glyph. This unique value specifies the position of the covered glyph in the Coverage table. The client uses the Coverage Index to look up values in the subtable for each glyph.
Coverage Format 1
Coverage Format 1 consists of a format code (CoverageFormat) and a count of covered glyphs (GlyphCount), followed by an array of glyph indices (GlyphArray). The glyph indices must be in numerical order for binary searching of the list. When a glyph is found in the Coverage table, its position in the GlyphArray determines the Coverage Index that is returned-the first glyph has a Coverage Index = 0, and the last glyph has a Coverage Index = GlyphCount -1.
Example 5 at the end of this chapter shows a Coverage table that uses Format 1 to list the GlyphIDs of all lowercase descender glyphs in a font.
CoverageFormat1 table: Individual glyph indices
| Type | Name | Description |
|---|---|---|
| uint16 | CoverageFormat | Format identifier-format = 1 |
| uint16 | GlyphCount | Number of glyphs in the GlyphArray |
| GlyphID | GlyphArray[GlyphCount] | Array of GlyphIDs-in numerical order |
Coverage Format 2
Format 2 consists of a format code (CoverageFormat) and a count of glyph index ranges (RangeCount), followed by an array of records (RangeRecords). Each RangeRecord consists of a start glyph index (Start), an end glyph index (End), and the Coverage Index associated with the range’s Start glyph. Ranges must be in GlyphID order, and they must be distinct, with no overlapping.
The Coverage Indexes for the first range begin with zero (0), and the Start Coverage Indexes for each succeeding range are determined by adding the length of the preceding range (End GlyphID - Start GlyphID + 1) to the array Index. This allows for a quick calculation of the Coverage Index for any glyph in any range using the formula: Coverage Index (GlyphID) = StartCoverageIndex + GlyphID - Start GlyphID.
Example 6 at the end of this chapter shows a Coverage table that uses Format 2 to identify a range of numeral glyphs in a font.
CoverageFormat2 table: Range of glyphs
| Type | Name | Description |
|---|---|---|
| uint16 | CoverageFormat | Format identifier-format = 2 |
| uint16 | RangeCount | Number of RangeRecords |
| struct | RangeRecord [RangeCount] |
Array of glyph ranges-ordered by Start GlyphID |
RangeRecord
| Type | Name | Description |
|---|---|---|
| GlyphID | Start | First GlyphID in the range |
| GlyphID | End | Last GlyphID in the range |
| uint16 | StartCoverageIndex | Coverage Index of first GlyphID in range |
Class Definition Table
In OpenType Layout, index values identify glyphs. For efficiency and ease of representation, a font developer can group glyph indices to form glyph classes. Class assignments vary in meaning from one lookup subtable to another. For example, in the GSUB and GPOS tables, classes are used to describe glyph contexts. GDEF tables also use the idea of glyph classes.
Consider a substitution action that replaces only the lowercase ascender glyphs in a glyph string. To more easily describe the appropriate context for the substitution, the font developer might divide the font’s lowercase glyphs into two classes, one that contains the ascenders and one that contains the glyphs without ascenders.
A font developer can assign any glyph to any class, each identified with an integer called a class value. A Class Definition table (ClassDef) groups glyph indices by class, beginning with Class 1, then Class 2, and so on. All glyphs not assigned to a class fall into Class 0. Within a given class definition table, each glyph in the font belongs to exactly one class.
The ClassDef table can have either of two formats: one that assigns a range of consecutive glyph indices to different classes, or one that puts groups of consecutive glyph indices into the same class.
Class Definition Table Format 1
The first class definition format (ClassDefFormat1) specifies a range of consecutive glyph indices and a list of corresponding glyph class values. This table is useful for assigning each glyph to a different class because the glyph indices in each class are not grouped together.
A ClassDef Format 1 table begins with a format identifier (ClassFormat). The range of glyph indices (GlyphIDs) covered by the table is identified by two values: the GlyphID of the first glyph (StartGlyph), and the number of consecutive GlyphIDs (including the first one) that will be assigned class values (GlyphCount). The ClassValueArray lists the class value assigned to each GlyphID, starting with the class value for StartGlyph and following the same order as the GlyphIDs. Any glyph not included in the range of covered GlyphIDs automatically belongs to Class 0.
Example 7 at the end of this chapter uses Format 1 to assign class values to the lowercase, x-height, ascender, and descender glyphs in a font.
ClassDefFormat1 table: Class array
| Type | Name | Description |
|---|---|---|
| uint16 | ClassFormat | Format identifier-format = 1 |
| GlyphID | StartGlyph | First GlyphID of the ClassValueArray |
| uint16 | GlyphCount | Size of the ClassValueArray |
| uint16 | ClassValueArray[GlyphCount] | Array of Class Values-one per GlyphID |
Class Definition Table Format 2
The second class definition format (ClassDefFormat2) defines multiple groups of glyph indices that belong to the same class. Each group consists of a discrete range of glyph indices in consecutive order (ranges cannot overlap).
The ClassDef Format 2 table contains a format identifier (ClassFormat), a count of ClassRangeRecords that define the groups and assign class values (ClassRangeCount), and an array of ClassRangeRecords ordered by the GlyphID of the first glyph in each record (ClassRangeRecord).
Each ClassRangeRecord consists of a Start glyph index, an End glyph index, and a Class value. All GlyphIDs in a range, from Start to End inclusive, constitute the class identified by the Class value. Any glyph not covered by a ClassRangeRecord is assumed to belong to Class 0.
Example 8 at the end of this chapter uses Format 2 to assign class values to four types of glyphs in the Arabic script.
ClassDefFormat2 table: Class ranges
| Type | Name | Description |
|---|---|---|
| uint16 | ClassFormat | Format identifier-format = 2 |
| uint16 | ClassRangeCount | Number of ClassRangeRecords |
| struct | ClassRangeRecord [ClassRangeCount] |
Array of ClassRangeRecords-ordered by Start GlyphID |
ClassRangeRecord
| Type | Name | Description |
|---|---|---|
| GlyphID | Start | First GlyphID in the range |
| GlyphID | End | Last GlyphID in the range |
| uint16 | Class | Applied to all glyphs in the range |
Device Tables
Glyphs in a font are defined in design units specified by the font developer. Font scaling increases or decreases a glyph’s size and rounds it to the nearest whole pixel. However, precise glyph positioning often requires adjustment of these scaled and rounded values. Hinting, applied to points in the glyph outline, is an effective solution to this problem, but it may require the font developer to redesign or re-hint glyphs.
Another solution-used by the GPOS, BASE, JSTF, and GDEF tables-is to use a Device table to specify correction values to adjust the scaled design units. A Device table applies the correction values to the range of sizes identified by StartSize and EndSize, which specify the smallest and largest pixel-per-em (ppem) sizes needing adjustment.
Because the adjustments often are very small (a pixel or two), the correction can be compressed into a 2-, 4-, or 8-bit representation per size. Two bits can represent a number in the range {-2, -1, 0, or 1}, four bits can represent a number in the range {-8 to 7}, and eight bits can represent a number in the range {-128 to 127}. The Device table identifies one of three data formats-signed 2-, 4,- or 8-bit values-for the adjustment values (DeltaFormat). A single Device table provides delta information for one coordinate at a range of sizes.
| Type | Name | Description |
|---|---|---|
| 1 | 2 | Signed 2-bit value, 8 values per uint16 |
| 2 | 4 | Signed 4-bit value, 4 values per uint16 |
| 3 | 8 | Signed 8-bit value, 2 values per uint16 |
The DeltaValue array lists the number of pixels to adjust specified points on the glyph, or the entire glyph, at each ppem size in the targeted range. In the array, the first index position specifies the number of pixels to add or subtract from the coordinate at the smallest ppem size that needs correction, the second index position specifies the number of pixels to add or subtract from the coordinate at the next ppem size, and so on for each ppem size in the range.
Example 9 at the end of this chapter uses a Device table to define the minimum extent value for a math script.
Device table
| Type | Name | Description |
|---|---|---|
| uint16 | StartSize | Smallest size to correct-in ppem |
| uint16 | EndSize | Largest size to correct-in ppem |
| uint16 | DeltaFormat | Format of DeltaValue array data: 1, 2, or 3 |
| uint16 | DeltaValue[ ] | Array of compressed data |
Common Table Examples
The rest of this chapter describes and illustrates examples of all the common table formats. All the examples reflect unique parameters, but the samples provide a useful reference for building tables specific to other situations.
The examples have three columns showing hex data, source, and comments.
Example 1: ScriptList Table and ScriptRecords
Example 1 illustrates a ScriptList table and ScriptRecord definitions for a Japanese font with multiple scripts: Han Ideographic, Kana, and Latin. Each script has script-specific behavior.
Example 1
| Hex Data | Source | Comment |
|---|---|---|
| ScriptList TheScriptList |
ScriptList table definintion | |
| 0003 | 3 | ScriptCount ScriptRecord[0],in alphabetical order by ScriptTag |
| 68616E69 | "hani" | ScriptTag, Han Ideographic script |
| 0014 | HanIScriptTable | offset to Script table ScriptRecord[1] |
| 6B616E61 | "kana" | ScriptTag, Hiragana and Katakana scripts |
| 0018 | KanaScriptTable | offset to Script table ScriptRecord[2] |
| 6C61746E | "latn" | ScriptTag, Latin script |
| 001C | LatinScriptTable | offset to Script table |
Example 2: Script Table, LangSysRecord, and LangSys Table
Example 2 illustrates the Script table, LangSysRecord, and LangSys table definitions for the Arabic script and the Urdu language system. The default LangSys table defines three default Arabic script features used to replace certain glyphs in words with their proper initial, medial, and final glyph forms. These contextual substitutions are invariant and occur in all language systems that use the Arabic script.
Many alternative glyphs in the Arabic script have language-specific uses. For instance, the Arabic, Farsi, and Urdu language systems use different glyphs for numerals. To maintain character-set compatibility, the Unicode standard includes separate character codes for the Arabic and Farsi numeral glyphs. However, the standard uses the same character codes for Farsi and Urdu numerals, even though three of the Urdu glyphs (4, 6, and 7) differ from the Farsi glyphs. To access and display the proper glyphs for the Urdu numerals, users of the text-processing client must enter the character codes for the Farsi numerals. Then the text-processing client uses a required OpenType Layout glyph substitution feature, defined in the Urdu LangSys table, to access the correct Urdu glyphs for the 4, 6, and 7 numerals.
Note that the Urdu LangSys table repeats the default script features. This repetition is necessary because the Urdu language system also uses alternative glyphs in the initial, medial, and final glyph positions in words.
Example 2
| Hex Data | Source | Comment |
|---|---|---|
| Script ArabicScriptTable |
Script table definition | |
| 000A | DefLangSys | offset to DefaultLangSys table |
| 0001 | 1 | LangSysCount LangSysRecord[0], in alphabetical order by LangSysTag |
| 55524420 | "URD " | LangSysTag, Urdu language |
| 0016 | UrduLangSys | offset to LangSys table for Urdu |
| LangSys DefLangSys |
default LangSys table definition | |
| 0000 | NULL | LookupOrder, reserved, null |
| FFFF | 0xFFFF | ReqFeatureIndex, no required features |
| 0003 | 3 | FeatureCount |
| 0000 | 0 | FeatureIndex[0], in arbitrary order "init" feature (initial glyph) |
| 0001 | 1 | FeatureIndex[1], "fina" feature (final glyph) |
| 0002 | 2 | FeatureIndex[2], for "medi" feature (medial glyph) |
| LangSys UrduLangSys |
LangSys table definition | |
| 0000 | NULL | LookupOrder, reserved, null |
| 0003 | 3 | ReqFeatureIndex, numeral subsitution in Urdu |
| 0003 | 3 | FeatureCount |
| 0000 | 0 | FeatureIndex[0], in arbitrary order "init" feature (initial glyph) |
| 0001 | 1 | FeatureIndex[1], "fina" feature (final glyph) |
| 0002 | 2 | FeatureIndex[2], "medi" feature (medial glyph) |
Example 3: FeatureList Table and Feature Table
Example 3 shows the FeatureList and Feature table definitions for ligatures in the Latin script. The FeatureList has three features, all optional and named "liga." One feature, also a default, implements ligatures in Latin if no language-specific feature specifies other ligatures. Two other features implement ligatures in the Turkish and German languages, respectively.
Three lookups define glyph substitutions for rendering ligatures in this font. The first lookup produces the "ffi" and "fi" ligatures; the second produces the "ffl," "fl," and "ff" ligatures; and the third produces the eszet ligature.
The ligatures that begin with an "f" are separated into two sets because Turkish has a dotless "i" glyph and so does not use "ffi" and "fi" ligatures. However, Turkish does use the "ffl," "fl," and "ff" ligatures, and the TurkishLigatures feature table lists this one lookup.
Only the German language system uses the eszet ligature, so the GermanLigatures feature table includes a lookup for rendering that ligature.
Because the Latin script can use both sets of ligatures, the DefaultLigatures feature table defines two LookupList indices: one for the "ffi" and "fi" ligatures, and one for the "ffl," "fl," and "ff" ligatures. If the text-processing client selects this feature, then the font applies both lookups.
Note that the TurkishLigatures and DefaultLigatures feature tables both list a LookupListIndex of one (1) for the "ffl," "fl," and "ff" ligatures lookup. This is because language-specific lookups override all default language-system lookups, and a language-system feature table must explicitly list all lookups that apply to the language.
Example 3
| Hex Data | Source | Comment |
|---|---|---|
| FeatureList TheFeatureList |
FeatureList table definition | |
| 0003 | 3 | FeatureCount FeatureRecord[0] |
| 6C696761 | "liga" | FeatureTag |
| 0014 | TurkishLigatures | offset to Feature table, FflFfFlLiga FeatureRecord[1] |
| 6C696761 | "liga" | FeatureTag |
| 001A | DefaultLigatures | offset to Feature table, FfiFiLiga, FflFfFlLiga FeatureRecord[2] |
| 6C696761 | "liga" | FeatureTag |
| 0022 | GermanLigatures | offset to Feature table, EszetLiga |
| Feature TurkishLigatures |
Feature table definition | |
| 0000 | NULL | FeatureParams, reserved, null |
| 0001 | 1 | LookupCount |
| 0000 | 1 | LookupListIndex[1], ffl, fl, ff ligature substitution Lookup |
| Feature DefaultLigatures |
Feature table definition | |
| 0000 | NULL | FeatureParams - reserved, null |
| 0002 | 2 | LookupCount |
| 0000 | 0 | LookupListIndex[0], in arbitrary order, ffi, fi ligatures |
| 0001 | 1 | LookupListIndex[1], ffl, fl, ff ligature substitution Lookup |
| Feature GermanLigatures |
Feature table definition | |
| 0000 | NULL | FeatureParams - reserved, null |
| 0001 | 3 | LookupCount |
| 0000 | 0 | LookupListIndex[0], in arbitrary order, ffi, fi ligatures |
| 0001 | 1 | LookupListIndex[1], ffl, fl, ff ligature substitution Lookup |
| 0002 | 2 | LookupListIndex[2], eszet ligature substitution Lookup |
Example 4: LookupList Table and Lookup Table
A continuation of Example 3, Example 4 shows three ligature lookups in the LookupList table. The first generates the "ffi" and "fi" ligatures; the second produces the "ffl," "fl," and "ff" ligatures; and the third generates the eszet ligature. Each lookup table defines an offset to a subtable that contains data for the ligature substitution.
Example 4
| Hex Data | Source | Comment |
|---|---|---|
| LookupList TheLookupList |
LookupList table definition | |
| 0003 | 3 | LookupCount |
| 0008 | FfiFiLookup | offset to Lookup[0] table, in design order |
| 0010 | FflFlFfLookup | offset to Lookup[1] table |
| 0018 | EszetLookup | offset to Lookup[2] table |
| Lookup FfiFiLookup |
Lookup[0] table definition | |
| 0004 | 4 | LookupType, ligature subst |
| 000C | 0x000C | LookupFlag, IgnoreLigatures, IgnoreMarks |
| 0001 | 1 | SubTableCount |
| 0018 | FfiFiSubtable | offset to FfiFi ligature substitution subtable |
| Lookup FflFlFfLookup |
Lookup[1] table definition | |
| 0004 | 4 | LookupType ligature subst |
| 000C | 0x000C | LookupFlag- IgnoreLigatures, IgnoreMarks |
| 0001 | 1 | SubTableCount |
| 0028 | FflFlFfSubtable | offset to FflFlFf ligature substitution subtable |
| Lookup EszetLookup |
Lookup[2] table definition | |
| 0004 | 4 | LookupType- ligature subst |
| 000C | 0x000C | LookupFlag- IgnoreLigatures, IgnoreMarks |
| 0001 | 1 | SubTableCount |
| 0038 | EszetSubtable | offset to Eszet ligature substitution subtable |
Example 5: CoverageFormat1 Table (GlyphID List)
Example 5 illustrates a Coverage table that lists the GlyphIDs of all lowercase descender glyphs in a font. The table uses the list format instead of the range format because the GlyphIDs for the descender glyphs are not consecutively ordered.
Example 5
| Hex Data | Source | Comment |
|---|---|---|
| CoverageFormat1 DescenderCoverage |
Coverage table definition | |
| 0001 | 1 | CoverageFormat lists |
| 0005 | 5 | GlyphCount |
| 0038 | gGlyphID | GlyphArray[0], in GlyphID order |
| 003B | jGlyphID | GlyphArray[1] |
| 0041 | pGlyphID | GlyphArray[2] |
| 0042 | qGlyphID | GlyphArray[3] |
| 004A | yGlyphID | GlyphArray[4] |
Example 6: CoverageFormat2 Table (GlyphID Ranges)
Example 6 shows a Coverage table that defines ten numeral glyphs (0 through 9). The table uses the range format instead of the list format because the GlyphIDs are ordered consecutively in the font. The StartCoverageIndex of zero (0) indicates that the first GlyphID, for the zero glyph, returns a Coverage Index of 0. The second GlyphID, for the numeral one (1) glyph, returns a Coverage Index of 1, and so on.
Example 6
| Hex Data | Source | Comment |
|---|---|---|
| CoverageFormat2 NumeralCoverage |
Coverage table definition | |
| 0002 | 2 | CoverageFormat, GlyphID ranges |
| 0001 | 1 | RangeCount RangeRecord[0] |
| 004E | 0glyphID | Start GlyphID |
| 0057 | 9glyphID | End GlyphID |
| 0000 | 0 | StartCoverageIndex, first CoverageIndex = 0 |
Example 7: ClassDefFormat1 Table (Class Array)
The ClassDef table in Example 7 assigns class values to the lowercase glyphs in a font. The x-height glyphs are in Class 0, the ascender glyphs are in Class 1, and the descender glyphs are in Class 2. The array begins with the index for the lowercase "a" glyph.
Example 7
| Hex Data | Source | Comment |
|---|---|---|
| ClassDefFormat1 LowercaseClassDef |
ClassDef table definition | |
| 0001 | 1 | ClassFormat |
| 0032 | aGlyphID | StartGlyph |
| 001A | 26 | GlyphCount |
| 0000 | 0 | aGlyph, Xheight Class 0 |
| 0001 | 1 | bGlyph, Ascender Class 1 |
| 0000 | 0 | cGlyph, Xheight Class 0 |
| 0001 | 1 | dGlyph, Ascender Class 1 |
| 0000 | 0 | eGlyph, Xheight Class 0 |
| 0001 | 1 | fGlyph, Ascender Class 1 |
| 0002 | 2 | gGlyph, Descender Class 2 |
| 0001 | 1 | hGlyph, Ascender Class 1 |
| 0000 | 0 | iGlyph, Ascender Class 1 |
| 0002 | 2 | jGlyph, Descender Class 2 |
| 0001 | 1 | kGlyph, Ascender Class 1 |
| 0001 | 1 | lGlyph, Ascender Class 1 |
| 0000 | 0 | mGlyph, Xheight Class 0 |
| 0000 | 0 | nGlyph, Xheight Class 0 |
| 0000 | 0 | oGlyph, Xheight Class 0 |
| 0002 | 2 | pGlyph, Descender Class 2 |
| 0002 | 2 | qGlyph, Descender Class 2 |
| 0000 | 0 | rGlyph, Xheight Class 0 |
| 0000 | 0 | sGlyph, Xheight Class 0 |
| 0001 | 1 | tGlyph, Ascender Class 1 |
| 0000 | 0 | uGlyph, Xheight Class 0 |
| 0000 | 0 | vGlyph, Xheight Class 0 |
| 0000 | 0 | wGlyph, Xheight Class 0 |
| 0000 | 0 | xGlyph, Xheight Class 0 |
| 0002 | 2 | yGlyph, Descender Class 2 |
| 0000 | 0 | zGlyph, Xheight Class 0 |
Example 8: ClassDefFormat2 Table (Class Ranges)
In Example 8, the ClassDef table assigns class values to four types of glyphs in the Arabic script: medium-height base glyphs, high base glyphs, very high base glyphs, and default mark glyphs. The table lists only Class 1, Class 2, and Class 3; all glyphs not explicitly assigned a class fall into Class 0.
The table uses the range format because the GlyphIDs in each class are ordered consecutively in the font. In the ClassRange array, ClassRange definitions are ordered by the Start glyph index in each range. The indices of the high base glyphs, defined in ClassRange[0], are first in the font and have a class value of 2. ClassRange[1] defines all the very high base glyphs and assigns a class value of 3. ClassRange[2] contains all default mark glyphs; the class value is 1. Class 0 consists of all the medium-height base glyphs, which are not explicitly assigned a class value.
Example 8
| Hex Data | Source | Comment |
|---|---|---|
| ClassDefFormat2 GlyphHeightClassDef |
Class table definition | |
| 0002 | 2 | Class Format ranges |
| 0003 | 3 | ClassRangeCount ClassRange[0], ordered by StartGlyphID |
| 0030 | tahGlyphID | Start first GlyphID in the range |
| 0031 | dhahGlyphID | End Last GlyphID in the range |
| 0002 | 2 | Class, high base glyphs, ClassRange[1] |
| 0040 | cafGlyphID | Start, first GlyphID in the range |
| 0041 | gafGlyphID | End, Last GlyphID in the range |
| 0003 | 3 | Class, very high base glyphs, ClassRange[2] |
| 00D2 | fathatanDefaultGlyphID | Start, first GlyphID in the range |
| 00D3 | dammatanDefaultGlyphID | End, Last GlyphID in the range |
| 0001 | 1 | Class default marks |
Example 9: Device Table
Example 9 defines the minimum extent value for a math script, using a Device table to adjust the value according to the size of the output font. Here, the Device table defines single-pixel adjustments for font sizes from 11 ppem to 15 ppem. The DeltaFormat is 1, which signifies a packed array of signed 2-bit values, eight values per uint16.
Example 9
| Hex Data | Source | Comment |
|---|---|---|
| DeviceTableFormat1 MinCoordDeviceTable |
Device Table definition | |
| 000B | 11 | StartSize, 11 ppem |
| 000F | 15 | EndSize, 15 ppem |
| 0001 | 1 | DeltaFormat signed 2 bit value, 8 values per uint16 |
| 1 | increase 11ppem by 1 pixel | |
| 1 | increase 12ppem by 1 pixel | |
| 1 | increase 13ppem by 1 pixel | |
| 1 | increase 14ppem by 1 pixel | |
| 5540 | 1 | increase 15ppem by 1 pixel |
Feedback
Coming soon: Throughout 2024 we will be phasing out GitHub Issues as the feedback mechanism for content and replacing it with a new feedback system. For more information see: https://aka.ms/ContentUserFeedback.
Submit and view feedback for