Estimating Correlation and Variance/Covariance Matrices
Important
This content is being retired and may not be updated in the future. The support for Machine Learning Server will end on July 1, 2022. For more information, see What's happening to Machine Learning Server?
The rxCovCor function in RevoScaleR calculates the covariance, correlation, or sum of squares/cross-product matrix for a set of variables in a .xdf file or data frame. The size of these matrices is determined by the number of variables rather than the number of observations, so typically the results can easily fit into memory in R. A broad category of analyses can be computed from some form of a cross-product matrix, for example, factor analysis and principal components.
A cross-product matrix is a matrix of the form X'X, where X represents an arbitrary set of raw or standardized variables. More generally, this matrix is of the form X'WX, where W is a diagonal weighting matrix.
Computing Cross-Product Matrices
While rxCovCor is the primary tool for computing covariance, correlation, and other cross-product matrices, you will seldom call it directly. Instead, it is generally simpler to use one of the following convenience functions:
- rxCov: Use rxCov to return the covariance matrix
- rxCor: Use rxCor to return the correlation matrix
- rxSSCP: Use rxSSCP to return the augmented cross-product matrix, that is, we first add a column of 1’s (if no weights are specified) or a column equaling the square root of the weights to the data matrix, and then compute the cross-product.
Computing a Correlation Matrix for Use in Factor Analysis
The 5% sample of the U.S. 2000 census has over 14 million observations. In this example, we compute the correlation matrix for 16 variables derived from variables in the data set for individuals over the age of 20. This correlation matrix is then used as input into the standard R factor analysis function, factanal.
First, we specify the name and location of the data set:
# Computing a Correlation Matrix for Use in Factor Analysis
bigDataDir <- "C:/MRS/Data"
bigCensusData <- file.path(bigDataDir, "Census5PCT2000.xdf"
Next, we can take a quick look at some basic demographic and socio-economic variables by calling rxSummary. (For more information on variables in the census data, see http://usa.ipums.org/usa-action/variables/group.) Throughout the analysis we use the probability weighting variable, perwt, and restrict the analysis to people over the age of 20.
The
blocksPerReadargument is ignored if run locally using R Client. Learn more...
rxSummary(~phone + speakeng + wkswork1 + incwelfr + incss + educrec + metro +
ownershd + marst + lingisol + nfams + yrsusa1 + movedin + racwht + age,
data = bigCensusData, blocksPerRead = 5, pweights = "perwt",
rowSelection = age > 20)
This call provides summary information about the variables in this weighted subsample, including cell counts for factor variables:
Call:
rxSummary(formula = ~phone + speakeng + wkswork1 + incwelfr +
incss + educrec + metro + ownershd + marst + lingisol + nfams +
yrsusa1 + movedin + racwht + age, data = censusData, pweights = "perwt",
rowSelection = age > 20, blocksPerRead = 5)
Summary Statistics Results for: ~phone + speakeng + wkswork1 + incwelfr
+ incss + educrec + metro + ownershd + marst + lingisol + nfams +
yrsusa1 + movedin + racwht + age
File name: C:\MRS\Data\Census5PCT2000.xdf
Probability weights: perwt
Number of valid observations: 9822124
Name Mean StdDev Min Max SumOfWeights MissingWeights
wkswork1 32.068473 23.2438663 0 52 196971131 0
incwelfr 61.155293 711.0955602 0 25500 196971131 0
incss 1614.604835 3915.7717233 0 26800 196971131 0
nfams 1.163434 0.5375238 1 48 196971131 0
yrsusa1 2.868573 9.0098343 0 90 196971131 0
age 46.813005 17.1797905 21 93 196971131 0
Category Counts for phone
Number of categories: 3
phone Counts
N/A 5611380
No, no phone available 3957030
Yes, phone available 187402721
Category Counts for speakeng
Number of categories: 10
speakeng Counts
N/A (Blank) 0
Does not speak English 2956934
Yes, speaks English... 0
Yes, speaks only English 162425091
Yes, speaks very well 17664738
Yes, speaks well 7713303
Yes, but not well 6211065
Unknown 0
Illegible 0
Blank 0
Category Counts for educrec
Number of categories: 10
educrec Counts
N/A or No schooling 0
None or preschool 2757363
Grade 1, 2, 3, or 4 1439820
Grade 5, 6, 7, or 8 10180870
Grade 9 4862980
Grade 10 5957922
Grade 11 5763456
Grade 12 63691961
1 to 3 years of college 55834997
4+ years of college 46481762
Category Counts for metro
Number of categories: 5
metro Counts
Not applicable 13829398
Not in metro area 32533836
In metro area, central city 32080416
In metro, area, outside central city 60836302
Central city status unknown 57691179
Category Counts for ownershd
Number of categories: 8
ownershd Counts
N/A 5611380
Owned or being bought 0
Check mark (owns?) 0
Owned free and clear 40546259
Owned with mortgage or loan 94626060
Rents 0
No cash rent 3169987
With cash rent 53017445
Category Counts for marst
Number of categories: 6
marst Counts
Married, spouse present 112784037
Married, spouse absent 5896245
Separated 4686951
Divorced 21474299
Widowed 14605829
Never married/single (N/A) 37523770
Category Counts for lingisol
Number of categories: 3
lingisol Counts
N/A (group quarters/vacant) 5611380
Not linguistically isolated 182633786
Linguistically isolated 8725965
Category Counts for movedin
Number of categories: 7
movedin Counts
NA 92708540
This year or last year 20107246
2-5 years ago 30328210
6-10 years ago 16959897
11-20 years ago 16406155
21-30 years ago 10339278
31+ years ago 10121805
Category Counts for racwht
Number of categories: 2
racwht Counts
No 40684944
Yes 156286187
Next we call the rxCor function, a convenience function for rxCovCor that returns just the Pearson’s correlation matrix for the variables specified. We make heavy use of the transforms argument to create a series of logical (or dummy) variables from factor variables to be used in the creation of the correlation matrix.
censusCor <- rxCor(formula=~poverty + noPhone + noEnglish + onSocialSecurity +
onWelfare + working + incearn + noHighSchool + inCity + renter +
noSpouse + langIsolated + multFamilies + newArrival + recentMove +
white + sei + older,
data = bigCensusData, pweightsb= "perwt", blocksPerRead = 5,
rowSelection = age > 20,
transforms= list(
noPhone = phone == "No, no phone available",
noEnglish = speakeng == "Does not speak English",
working = wkswork1 > 20,
onWelfare = incwelfr > 0,
onSocialSecurity = incss > 0,
noHighSchool =
!(educrec %in%
c("Grade 12", "1 to 3 years of college", "4+ years of college")),
inCity = metro == "In metro area, central city",
renter = ownershd %in% c("No cash rent", "With cash rent"),
noSpouse = marst != "Married, spouse present",
langIsolated = lingisol == "Linguistically isolated",
multFamilies = nfams > 2,
newArrival = yrsusa2 == "0-5 years",
recentMove = movedin == "This year or last year",
white = racwht == "Yes",
older = age > 64
))
The resulting correlation matrix is used as input into the factor analysis function provided by the stats package in R. In interpreting the results, the variable poverty represents family income as a percentage of a poverty threshold, so increases as family income increases. First, specify two factors:
censusFa <- factanal(covmat = censusCor, factors=2)
print(censusFa, digits=2, cutoff = .2, sort= TRUE)
Results in:
Call:
factanal(factors = 2, covmat = censusCor)
Uniquenesses:
poverty noPhone noEnglish onSocialSecurity
0.53 0.96 0.93 0.23
onWelfare working incearn noHighSchool
0.96 0.51 0.68 0.82
inCity renter noSpouse langIsolated
0.97 0.79 0.90 0.90
multFamilies newArrival recentMove white
0.96 0.93 0.97 0.88
sei older
0.57 0.24
Loadings:
Factor1 Factor2
onSocialSecurity 0.83 -0.29
working -0.68
sei -0.59 -0.29
older 0.82 -0.29
poverty -0.28 -0.63
noPhone
noEnglish 0.26
onWelfare
incearn -0.46 -0.34
noHighSchool 0.31 0.29
inCity
renter 0.45
noSpouse 0.28
langIsolated 0.31
multFamilies
newArrival 0.26
recentMove
white -0.34
Factor1 Factor2
SS loadings 2.60 1.67
Proportion Var 0.14 0.09
Cumulative Var 0.14 0.24
The degrees of freedom for the model is 118 and the fit was 0.6019
We can use the same correlation matrix to estimate three factors:
censusFa <- factanal(covmat = censusCor, factors=3)
print(censusFa, digits=2, cutoff = .2, sort= TRUE)
Call:
factanal(factors = 3, covmat = censusCor)
Uniquenesses:
poverty noPhone noEnglish onSocialSecurity
0.49 0.96 0.72 0.24
onWelfare working incearn noHighSchool
0.96 0.50 0.62 0.80
inCity renter noSpouse langIsolated
0.96 0.80 0.90 0.59
multFamilies newArrival recentMove white
0.96 0.79 0.97 0.88
sei older
0.56 0.22
Loadings:
Factor1 Factor2 Factor3
onSocialSecurity 0.87
working -0.62 0.34
sei -0.51 0.42
older 0.88
poverty 0.68
incearn -0.36 0.51
noEnglish 0.53
langIsolated 0.64
noPhone
onWelfare -0.21
noHighSchool 0.25 -0.26 0.26
inCity
renter -0.36 0.24
noSpouse -0.30
multFamilies
newArrival 0.46
recentMove
white 0.24 -0.24
Factor1 Factor2 Factor3
SS loadings 2.41 1.50 1.18
Proportion Var 0.13 0.08 0.07
Cumulative Var 0.13 0.22 0.28
The degrees of freedom for the model is 102 and the fit was 0.343
Computing A Covariance Matrix for Principal Components Analysis
Principal components analysis, or PCA, is a technique closely related to factor analysis. PCA seeks to find a set of orthogonal axes such that the first axis, or first principal component, accounts for as much variability as possible, and subsequent axes or components are chosen to maximize variance while maintaining orthogonality with previous axes. Principal components are typically computed either by a singular value decomposition of the data matrix or an eigenvalue decomposition of a covariance or correlation matrix; the latter permits us to use rxCovCor and its relatives with the standard R function princomp.
As an example, we use the rxCov function to calculate a covariance matrix for the log of the classic iris data, and pass the matrix to the princomp function (reproduced from Modern Applied Statistics with S):
# Computing A Covariance Matrix for Principal Components Analysis
irisLog <- as.data.frame(lapply(iris[,1:4], log))
irisSpecies <- iris[,5]
irisCov <- rxCov(~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
data=irisLog)
irisPca <- princomp(covmat=irisCov, cor=TRUE)
summary(irisPca)
Yields the following:
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.7124583 0.9523797 0.36470294 0.1656840
Proportion of Variance 0.7331284 0.2267568 0.03325206 0.0068628
Cumulative Proportion 0.7331284 0.9598851 0.99313720 1.0000000
The default plot method for objects of class princomp is a scree plot, which is a barplot of the variances of the principal components. We can obtain the plot as usual by calling plot with our principal components object:
plot(irisPca)
Yields the following plot:
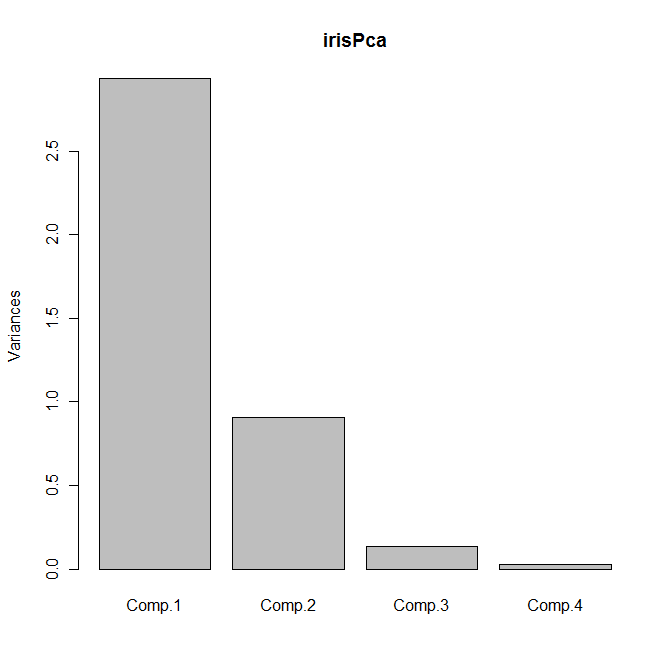
Another useful bit of output is given by the loadings function, which returns a set of columns showing the linear combinations for each principal component:
loadings(irisPca)
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
Sepal.Length 0.504 -0.455 0.709 0.191
Sepal.Width -0.302 -0.889 -0.331
Petal.Length 0.577 -0.219 -0.786
Petal.Width 0.567 -0.583 0.580
Comp.1 Comp.2 Comp.3 Comp.4
SS loadings 1.00 1.00 1.00 1.00
Proportion Var 0.25 0.25 0.25 0.25
Cumulative Var 0.25 0.50 0.75 1.00
You may have noticed that we supplied the flag cor=TRUE in the call to princomp; this flag tells princomp to use the correlation matrix rather than the covariance matrix to compute the principal components. We can obtain the same results by omitting the flag but submitting the correlation matrix as returned by rxCor instead:
irisCor <- rxCor(~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
data=irisLog)
irisPca2 <- princomp(covmat=irisCor)
summary(irisPca2)
loadings(irisPca2)
plot(irisPca2)
A Large Data Principal Components Analysis
Stock market data for open, high, low, close, and adjusted close from 1962 to 2010 is available at https://github.com/thebigjc/HackReduce/blob/master/datasets/nyse/daily_prices/NYSE_daily_prices_subset.csv. The full data set includes 9.2 million observations of daily open-high-low-close data for some 2800 stocks. As you might expect, these data are highly correlated, and principal components analysis can be used for data reduction. We read the original data into a .xdf file, NYSE_daily_prices.xdf, using the same process we used in the Tutorial: Analyzing loan data with RevoScaleR to read our mortgage data (set revoDataDir to the full path to the NYSE directory containing the .csv files when you unpack the download):
# A Large Data Principal Components Analysis
if (bHasNYSE){
bigDataDir <- "C:/MRS/Data"
nyseCsvFiles <- file.path(bigDataDir, "NYSE_daily_prices","NYSE",
"NYSE_daily_prices_")
nyseXdf <- "NYSE_daily_prices.xdf"
append <- "none"
for (i in LETTERS)
{
importFile <- paste(nyseCsvFiles, i, ".csv", sep="")
rxImport(importFile, nyseXdf, append=append)
append <- "rows"
}
Once we have our .xdf file, we proceed as before:
stockCor <- rxCor(~ stock_price_open + stock_price_high +
stock_price_low + stock_price_close +
stock_price_adj_close, data="NYSE_daily_prices.xdf")
stockPca <- princomp(covmat=stockCor)
summary(stockPca)
loadings(stockPca)
plot(stockPca)
Yields the following output:
> summary(stockPca)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 2.0756631 0.8063270 0.197632281 0.0454173922
Proportion of Variance 0.8616755 0.1300327 0.007811704 0.0004125479
Cumulative Proportion 0.8616755 0.9917081 0.999519853 0.9999324005
Comp.5
Standard deviation 1.838470e-02
Proportion of Variance 6.759946e-05
Cumulative Proportion 1.000000e+00
> loadings(stockPca)
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
stock_price_open -0.470 -0.166 0.867
stock_price_high -0.477 -0.151 -0.276 0.410 -0.711
stock_price_low -0.477 -0.153 -0.282 0.417 0.704
stock_price_close -0.477 -0.149 -0.305 -0.811
stock_price_adj_close -0.309 0.951
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
SS loadings 1.0 1.0 1.0 1.0 1.0
Proportion Var 0.2 0.2 0.2 0.2 0.2
Cumulative Var 0.2 0.4 0.6 0.8 1.0
The scree plot is shown as follows:
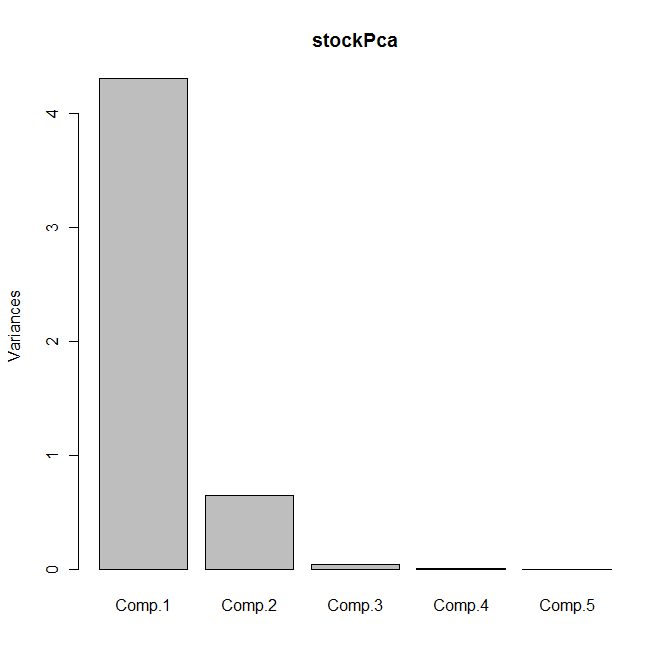
Between them, the first two principal components explain 99% of the variance; we can therefore replace the five original variables by these two principal components with no appreciable loss of information.
Ridge Regression
Another application of correlation matrices is to calculate ridge regression, a type of regression that can help deal with multicollinearity and is part of a broader class of models called Penalized Regression Models.
Where the ordinary least squares regression minimizes the sum of squared residuals

ridge regression minimizes the slightly modified sum

The solution to the ridge regression is

where  is the model matrix. This matrix is similar to the ordinary least squares regression solution with a “ridge” added along the diagonal.
is the model matrix. This matrix is similar to the ordinary least squares regression solution with a “ridge” added along the diagonal.
Since the model matrix is embedded in the correlation matrix, the following function allows us to compute the ridge regression solution:
# Ridge regression
rxRidgeReg <- function(formula, data, lambda, ...) {
myTerms <- all.vars(formula)
newForm <- as.formula(paste("~", paste(myTerms, collapse = "+")))
myCor <- rxCovCor(newForm, data = data, type = "Cor", ...)
n <- myCor$valid.obs
k <- nrow(myCor$CovCor) - 1
bridgeprime <- do.call(rbind, lapply(lambda,
function(l) qr.solve(myCor$CovCor[-1,-1] + l*diag(k),
myCor$CovCor[-1,1])))
bridge <- myCor$StdDevs[1] * sweep(bridgeprime, 2,
myCor$StdDevs[-1], "/")
bridge <- cbind(t(myCor$Means[1] -
tcrossprod(myCor$Means[-1], bridge)), bridge)
rownames(bridge) <- format(lambda)
return(bridge)
}
The following example shows how ridge regression dramatically improves the solution in a regression involving heavy multicollinearity:
set.seed(14)
x <- rnorm(100)
y <- rnorm(100, mean=x, sd=.01)
z <- rnorm(100, mean=2 + x +y)
data <- data.frame(x=x, y=y, z=z)
lm(z ~ x + y)
Call:
lm(formula = z ~ x + y)
Coefficients:
(Intercept) x y
1.827 4.359 -2.584
rxRidgeReg(z ~ x + y, data=data, lambda=0.02)
x y
0.02 1.827674 0.8917924 0.8723334
You can supply a vector of lambdas as a quick way to compare various choices:
rxRidgeReg(z ~ x + y, data=data, lambda=c(0, 0.02, 0.2, 2, 20))
x y
0.00 1.827112 4.35917238 -2.58387778
0.02 1.827674 0.89179239 0.87233344
0.20 1.833899 0.81020130 0.80959911
2.00 1.865339 0.44512940 0.44575060
20.00 1.896779 0.08092296 0.08105322
For λ = 0, the ridge regression is identical to ordinary least squares, while as λ → ∞, the coefficients of x and y approach 0.