Bináris besorolás
A besorolás, mint a regresszió, felügyelt gépi tanulási technika, ezért ugyanazt az iteratív folyamatot követi a betanítás, a validálás és a modellek kiértékelése során. Ahelyett, hogy numerikus értékeket, például regressziós modellt számítanak ki, a besorolási modellek betanításához használt algoritmusok kiszámítják az osztály-hozzárendelés valószínűségi értékeit, és a modell teljesítményének értékeléséhez használt kiértékelési metrikák összehasonlítják az előrejelzett osztályokat a tényleges osztályokkal.
A bináris besorolási algoritmusok olyan modellek betanítása, amelyek egy osztály két lehetséges címkéjének egyikét jelzik előre. Lényegében igaz vagy hamis előrejelzés. A legtöbb valós forgatókönyvben a modell betanítása és ellenőrzése során használt adatmegfigyelések több funkcióértékből (x) és egy 1 vagy 0 értékű y értékből állnak.
Példa – bináris besorolás
A bináris besorolás működésének megértéséhez tekintsünk meg egy egyszerűsített példát, amely egyetlen funkcióval (x) jelzi előre, hogy az y címke 1 vagy 0. Ebben a példában a páciens vércukorszintjének előrejelzésére használjuk, hogy a beteg cukorbeteg-e vagy sem. Az alábbi adatokkal tanítjuk be a modellt:
 |
 |
|---|---|
| Vércukorszint (x) | Diabéteszes? (y) |
| 67 | 0 |
| 103 | 0 |
| 114 | 0 |
| 72 | 0 |
| 116 | 0 |
| 65 | 0 |
Bináris besorolási modell betanítása
A modell betanításához egy algoritmussal illesztjük be a betanítási adatokat egy olyan függvényhez, amely kiszámítja az osztálycímke igaz valószínűségét (vagyis azt, hogy a beteg cukorbetegségben szenved). A valószínűség 0,0 és 1,0 közötti értékként van megadva, így az összes lehetséges osztály teljes valószínűsége 1,0. Így például, ha a diabéteszes beteg valószínűsége 0,7, akkor 0,3-nak megfelelő valószínűsége van annak, hogy a beteg nem cukorbeteg.
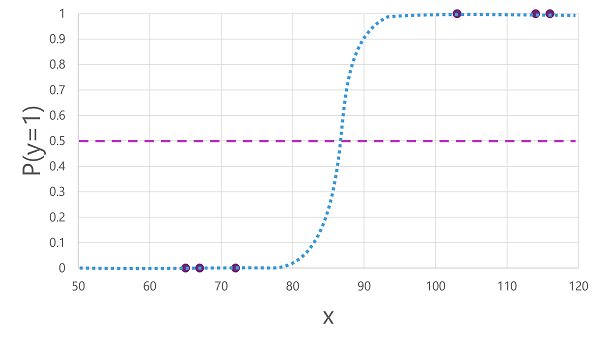
Számos algoritmus használható bináris besoroláshoz, például logisztikai regresszióhoz, amely egy szigmoid (S-alakú) függvényt hoz létre 0,0 és 1,0 közötti értékekkel, például a következőhöz hasonlóan:
Feljegyzés
A neve ellenére a gépi tanulásban a logisztikai regressziót a besoroláshoz, nem a regresszióhoz használják. A fontos pont az általa előállított függvény logisztikai jellege, amely egy S alakú görbét ír le egy alsó és egy felső érték között (bináris besorolás esetén 0,0 és 1,0).
Az algoritmus által előállított függvény az y valószínűségét írja le (y=1) egy adott x értékre. Matematikailag így fejezheti ki a függvényt:
f(x) = P(y=1 | x)
A betanítási adatokban szereplő hat megfigyelés közül három esetében tudjuk, hogy az y határozottan igaz, így az y=1 megfigyelések valószínűsége 1,0, a másik három esetében pedig azt, hogy az y határozottan hamis, tehát az y=1 valószínűsége 0,0. Az S-alakú görbe a valószínűségeloszlást írja le, így az x érték ábrázolása a vonalon azonosítja az y valószínűségét 1.
A diagram egy vízszintes vonalat is tartalmaz, amely jelzi azt a küszöbértéket, amelynél a függvényen alapuló modell true (1) vagy false (0) értéket jelez előre. A küszöbérték az y (P(y) = 0,5) középpontján található. Az ezen a ponton vagy annál magasabb értékeknél a modell igaz értéket (1) jelez előre, míg a pont alatti értékek esetében hamis (0) értéket jelez előre. Például egy 90-es vércukorszinttel rendelkező betegnél a függvény 0,9-es valószínűségi értéket eredményezne. Mivel a 0,9 magasabb, mint a 0,5 küszöbérték, a modell igaz (1) előrejelzést adna - más szóval, a betegnek cukorbetegsége van.
Bináris besorolási modell kiértékelése
A regresszióhoz hasonlóan a bináris besorolási modellek betanításakor az adatok egy véletlenszerű részhalmazát is visszatartja, amellyel érvényesítheti a betanított modellt. Tegyük fel, hogy az alábbi adatokat visszatartottuk a cukorbetegség-osztályozó ellenőrzéséhez:
| Vércukorszint (x) | Diabéteszes? (y) |
|---|---|
| 66 | 0 |
| 107 | 0 |
| 112 | 0 |
| 71 | 0 |
| 87 | 0 |
| 89 | 0 |
A korábban az x értékekre származtatott logisztikai függvény alkalmazása az alábbi ábrát eredményezi.
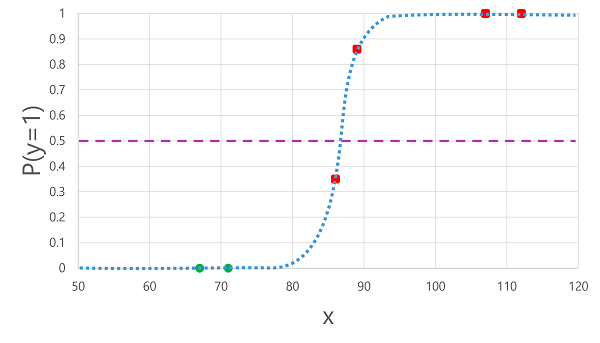
Attól függően, hogy a függvény által kiszámított valószínűség a küszöbérték felett vagy alatt van-e, a modell minden megfigyeléshez 1 vagy 0 előrejelzett címkét hoz létre. Ezután összehasonlíthatjuk az előrejelzett osztályfeliratokat (ŷ) a tényleges osztálycímkékkel (y), ahogy az itt látható:
| Vércukorszint (x) | A cukorbetegség tényleges diagnosztizálása (y) | Előrejelzett cukorbetegség diagnosztizálása (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 0 | 0 |
| 112 | 0 | 0 |
| 71 | 0 | 0 |
| 87 | 0 | 0 |
| 89 | 0 | 0 |
Bináris besorolás kiértékelési mérőszámai
A bináris besorolási modellek kiértékelési metrikáinak kiszámításának első lépése általában az egyes lehetséges osztálycímkék helyes és helytelen előrejelzéseinek számának mátrixának létrehozása:
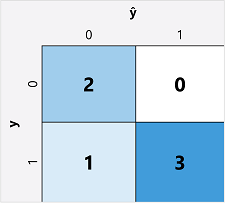
Ezt a vizualizációt keveredési mátrixnak nevezzük, és megjeleníti az előrejelzési összegeket, ahol:
- ŷ=0 és y=0: Igaz negatívok (TN)
- ŷ=1 és y=0: Hamis pozitív értékek (FP)
- ŷ=0 és y=1: Hamis negatívok (FN)
- ŷ=1 és y=1: Igaz pozitívok (TP)
A keveredési mátrix elrendezése olyan, hogy a helyes (igaz) előrejelzések a bal felső és a jobb alsó sarok közötti átlós vonalban jelennek meg. A színintenzitást gyakran használják az egyes cellákban lévő előrejelzések számának jelzésére, ezért egy jól előrejelző modell gyors áttekintése egy mélyen árnyékolt átlós trendet jelenít meg.
Pontosság
A keveredési mátrixból kiszámítható legegyszerűbb metrika a pontosság – a modell által helyesen kapott előrejelzések aránya. A pontosság kiszámítása a következőképpen történik:
(TN+TP) ÷ (TN+FN+FP+TP)
Diabéteszes példánk esetében a számítás a következő:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0.83
Az ellenőrzési adatok alapján a cukorbetegség besorolási modellje az idő 83%-ában helyes előrejelzéseket hozott létre.
A pontosság kezdetben jó metrikának tűnhet egy modell kiértékeléséhez, de fontolja meg ezt. Tegyük fel, hogy a lakosság 11%-ának cukorbetegsége van. Létrehozhat egy modellt, amely mindig 0-t jelez előre, és 89%-os pontosságot érne el, annak ellenére, hogy nem tesz valódi kísérletet a betegek megkülönböztetésére a jellemzőik kiértékelésével. Amire igazán szükségünk van, az az, hogy jobban megértsük, hogyan teljesít a modell az 1 pozitív esetekre és 0 negatív esetekre történő előrejelzéséhez.
Visszavonás
A visszahívás egy olyan metrika, amely a modell által helyesen azonosított pozitív esetek arányát méri. Más szóval, összehasonlítva a cukorbetegek számával, hányat jósol a modell a cukorbetegségre?
A visszahívás képlete a következő:
TP ÷ (TP+FN)
Diabéteszes példánkhoz:
3 ÷ (3+1)
= 3 ÷ 4
= 0.75
Tehát a modellünk helyesen azonosította a cukorbetegek 75% -át cukorbetegségnek.
Pontosság
A pontosság hasonló a visszahíváshoz, de az előrejelzett pozitív esetek arányát méri, ahol a valódi címke valójában pozitív. Más szóval, milyen arányban a betegek előre a modell, hogy a cukorbetegség valójában cukorbetegség?
A pontosság képlete a következő:
TP ÷ (TP+FP)
Diabéteszes példánkhoz:
3 ÷ (3+0)
= 3 ÷ 3
= 1.0
Tehát a modellünk által előrejelzett betegek 100%-ának cukorbetegsége van.
F1-pontszám
Az F1-pontszám egy általános metrika, amely a visszahívást és a pontosságot kombinálja. Az F1-pontszám képlete:
(2 x Pontosság x visszahívás) ÷ (Pontosság + Visszahívás)
Diabéteszes példánkhoz:
(2 x 1,0 x 0,75) ÷ (1,0 + 0,75)
= 1,5 ÷ 1,75
= 0,86
A görbe alatti terület (AUC)
A visszahívás másik neve a valódi pozitív arány (TPR), és létezik egy egyenértékű metrika, az úgynevezett hamis pozitív ráta (FPR), amelyet FP÷(FP+TN) értékként számítunk ki. Már tudjuk, hogy a modell 0,5-ös küszöbérték használatakor a TPR értéke 0,75, és az FPR képletével kiszámíthatjuk a 0÷2 = 0 értéket.
Természetesen ha módosítanánk azt a küszöbértéket, amely felett a modell igaz (1) előrejelzést adna, az hatással lenne a pozitív és negatív előrejelzések számára, és ezért megváltoztatná a TPR- és FPR-metrikákat. Ezeket a metrikákat gyakran használják a modell kiértékelésére egy fogadott operátori jellemző (ROC) görbe ábrázolásával, amely összehasonlítja a TPR és az FPR értékét minden lehetséges küszöbérték 0,0 és 1,0 között:
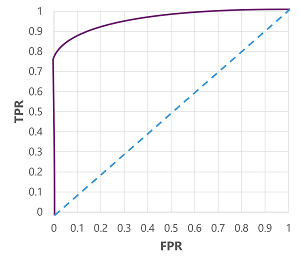
A tökéletes modell ROC-görbéje egyenesen felfelé halad a bal oldali TPR tengelyen, majd felül az FPR tengelyen. Mivel a görbe ábrázolási területe 1x1, a tökéletes görbe alatti terület 1,0 lenne (ami azt jelenti, hogy a modell az idő 100%-ában helyes). Ezzel szemben a bal alsó és a jobb felső sarok közötti átlós vonal azokat az eredményeket jelöli, amelyeket egy bináris címke véletlenszerű kitalálásával lehetne elérni; 0,5 görbe alatti területet hoz létre. Más szóval, két lehetséges osztálycímkével, ésszerűen számíthat arra, hogy az idő 50%-át helyesen kitalálja.
Cukorbetegség-modellünk esetében a fenti görbe jön létre, a görbe alatti terület (AUC) metrika pedig 0,875. Mivel az AUC magasabb, mint 0,5, azt a következtetést vonhatjuk le, hogy a modell jobban teljesít annak előrejelzésében, hogy egy beteg cukorbetegségben szenved-e, mint véletlenszerűen kitalálva.