Gambaran umum transformasi

Transformasi matriks menangani banyak matematika tingkat rendah dari grafik 3D.

Alur geometri mengambil simpul sebagai input. Mesin transformasi menerapkan dunia, tampilan, dan proyeksi berubah ke simpul, mengklip hasilnya, dan meneruskan semuanya ke rasterizer.

Transformasi dan spasi	Deskripsi
Koordinat model dalam ruang model	Di kepala alur, simpul model dinyatakan relatif terhadap sistem koordinat lokal. Ini adalah asal lokal dan orientasi. Orientasi koordinat ini sering disebut sebagai ruang model. Koordinat individual disebut koordinat model.
Dunia berubah menjadi ruang dunia	Tahap pertama alur geometri mengubah simpul model dari sistem koordinat lokal mereka ke sistem koordinat yang digunakan oleh semua objek dalam adegan. Proses reorientasi puncak disebut transformasi Dunia, yang berubah dari ruang model ke orientasi baru yang disebut ruang dunia. Setiap puncak di ruang dunia dideklarasikan menggunakan koordinat dunia.
Lihat transformasi menjadi ruang tampilan (ruang kamera)	Pada tahap berikutnya, simpul yang menggambarkan dunia 3D Anda berorientasi pada kamera. Artinya, aplikasi Anda memilih titik pandang untuk adegan, dan koordinat ruang dunia direlokasi dan diputar di sekitar tampilan kamera, mengubah ruang dunia menjadi ruang pandang (juga dikenal sebagai ruang kamera). Ini adalah transformasi Tampilan, yang dikonversi dari ruang dunia untuk melihat ruang.
Proyeksi berubah menjadi ruang proyeksi	Tahap berikutnya adalah transformasi Proyeksi, yang dikonversi dari ruang tampilan ke ruang proyeksi. Di bagian alur ini, objek biasanya diskalakan dengan kaitannya dengan jaraknya dari penampil untuk memberikan ilusi kedalaman ke adegan; objek dekat dibuat agar tampak lebih besar dari objek yang jauh. Untuk kesederhanaan, dokumentasi ini mengacu pada ruang di mana simpul ada setelah proyeksi berubah sebagai ruang proyeksi. Beberapa buku grafis mungkin menyebut ruang proyeksi sebagai ruang homogen pasca-perspektif. Tidak semua proyeksi mengubah skala ukuran objek dalam adegan. Proyeksi seperti ini terkadang disebut proyeksi affine atau ortogonal.
Mengklip di ruang layar	Di bagian akhir alur, simpul apa pun yang tidak akan terlihat di layar dihapus, sehingga rasterizer tidak meluangkan waktu untuk menghitung warna dan bayangan untuk sesuatu yang tidak akan pernah terlihat. Proses ini disebut kliping. Setelah kliping, simpul yang tersisa diskalakan sesuai dengan parameter viewport dan dikonversi menjadi koordinat layar. Simpul yang dihasilkan, terlihat di layar ketika adegan dirasterisasi, ada di ruang layar.

 

Transformasi digunakan untuk mengonversi geometri objek dari satu ruang koordinat ke ruang koordinat lainnya. Direct3D menggunakan matriks untuk melakukan transformasi 3D. Matriks membuat transformasi 3D. Anda dapat menggabungkan matriks untuk menghasilkan satu matriks yang mencakup beberapa transformasi.

Anda dapat mengubah koordinat antara ruang model, ruang dunia, dan ruang tampilan.

• Transformasi dunia - Mengonversi dari ruang model ke ruang dunia.
• Lihat transformasi - Mengonversi dari ruang dunia untuk melihat ruang.
• Transformasi proyeksi - Mengonversi dari ruang tampilan ke ruang proyeksi.

Transformasi Matriks

Dalam aplikasi yang bekerja dengan grafik 3D, Anda dapat menggunakan transformasi geometris untuk melakukan hal berikut:

• Mengekspresikan lokasi objek relatif terhadap objek lain.
• Putar dan ukuran objek.
• Ubah posisi tampilan, arah, dan perspektif.

Anda dapat mengubah titik apa pun (x,y,z) menjadi titik lain (x', y', z') dengan menggunakan matriks 4x4, seperti yang ditunjukkan dalam persamaan berikut.

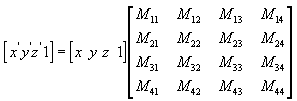
Lakukan persamaan berikut pada (x, y, z) dan matriks untuk menghasilkan titik (x', y', z').

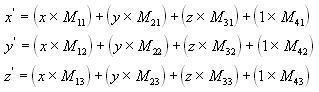
Transformasi yang paling umum adalah terjemahan, rotasi, dan penskalaan. Anda dapat menggabungkan matriks yang menghasilkan efek ini menjadi satu matriks untuk menghitung beberapa transformasi sekaligus. Misalnya, Anda dapat membuat satu matriks untuk menerjemahkan dan memutar serangkaian titik.

Matriks ditulis dalam urutan kolom baris. Matriks yang secara merata menskalakan simpul di sepanjang setiap sumbu, yang dikenal sebagai penskalaan seragam, diwakili oleh matriks berikut menggunakan notasi matematika.

Dalam C++, Direct3D mendeklarasikan matriks sebagai array dua dimensi, menggunakan struct matriks. Contoh berikut menunjukkan cara menginisialisasi struktur D3DMATRIX untuk bertindak sebagai matriks penskalakan seragam (faktor skala "s").

D3DMATRIX scale = {
    5.0f,            0.0f,            0.0f,            0.0f,
    0.0f,            5.0f,            0.0f,            0.0f,
    0.0f,            0.0f,            5.0f,            0.0f,
    0.0f,            0.0f,            0.0f,            1.0f
};

Menerjemahkan

Persamaan berikut menerjemahkan titik (x, y, z) ke titik baru (x', y', z').

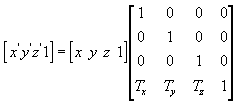
Anda dapat membuat matriks terjemahan secara manual di C++. Contoh berikut menunjukkan kode sumber untuk fungsi yang membuat matriks untuk menerjemahkan simpul.

D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
    D3DXMATRIX ret;

    D3DXMatrixIdentity(&ret);
    ret(3, 0) = dx;
    ret(3, 1) = dy;
    ret(3, 2) = dz;
    return ret;
}    // End of Translate

Skala

Persamaan berikut menskalakan titik (x, y, z) dengan nilai arbitrer dalam x-, y-, dan z-directions ke titik baru (x', y', z').

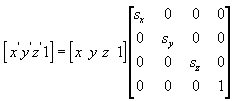
Memutar

Transformasi yang dijelaskan di sini adalah untuk sistem koordinat sebelah kiri, sehingga mungkin berbeda dari matriks transformasi yang telah Anda lihat di tempat lain.

Persamaan berikut memutar titik (x, y, z) di sekitar sumbu x, menghasilkan titik baru (x', y', z').

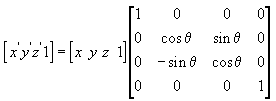
Persamaan berikut memutar titik di sekitar sumbu y.

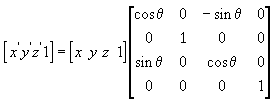
Persamaan berikut memutar titik di sekitar sumbu z.

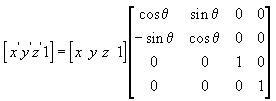
Dalam contoh matriks ini, theta huruf Yunani adalah singkatan dari sudut rotasi, dalam radian. Sudut diukur searah jarang saat melihat sepanjang sumbu rotasi menuju asal.

Kode berikut menunjukkan fungsi untuk menangani rotasi tentang sumbu X.

    // Inputs are a pointer to a matrix (pOut) and an angle in radians.
    float sin, cos;
    sincosf(angle, &sin, &cos);  // Determine sin and cos of angle

    pOut->_11 = 1.0f; pOut->_12 =  0.0f;   pOut->_13 = 0.0f; pOut->_14 = 0.0f;
    pOut->_21 = 0.0f; pOut->_22 =  cos;    pOut->_23 = sin;  pOut->_24 = 0.0f;
    pOut->_31 = 0.0f; pOut->_32 = -sin;    pOut->_33 = cos;  pOut->_34 = 0.0f;
    pOut->_41 = 0.0f; pOut->_42 =  0.0f;   pOut->_43 = 0.0f; pOut->_44 = 1.0f;

    return pOut;
}

Menggabungkan Matriks

Salah satu keuntungan menggunakan matriks adalah Anda dapat menggabungkan efek dari dua matriks atau lebih dengan mengalikannya. Ini berarti bahwa, untuk memutar model dan kemudian menerjemahkannya ke beberapa lokasi, Anda tidak perlu menerapkan dua matriks. Sebagai gantinya, Anda mengalikan matriks rotasi dan terjemahan untuk menghasilkan matriks komposit yang berisi semua efeknya. Proses ini, yang disebut perangkaian matriks, dapat ditulis dengan persamaan berikut.

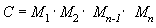
Dalam persamaan ini, C adalah matriks komposit yang dibuat, dan M₁ melalui Mn adalah matriks individu. Dalam kebanyakan kasus, hanya dua atau tiga matriks yang digabungkan, tetapi tidak ada batasan.

Urutan di mana perkalian matriks dilakukan sangat penting. Rumus sebelumnya mencerminkan aturan kiri-ke-kanan dari perangkaian matriks. Artinya, efek matriks yang terlihat yang Anda gunakan untuk membuat matriks komposit terjadi dalam urutan kiri-ke-kanan. Matriks dunia yang khas ditampilkan dalam contoh berikut. Bayangkan bahwa Anda menciptakan matriks dunia untuk piring terbang stereotip. Anda mungkin ingin memutar pelau terbang di sekitar pusatnya - sumbu y ruang model - dan menerjemahkannya ke beberapa lokasi lain di adegan Anda. Untuk mencapai efek ini, Anda terlebih dahulu membuat matriks rotasi, lalu mengalikannya dengan matriks terjemahan, seperti yang ditunjukkan dalam persamaan berikut.

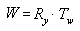
Dalam rumus ini, R_y adalah matriks untuk rotasi tentang sumbu y, dan T_w adalah terjemahan ke beberapa posisi dalam koordinat dunia.

Urutan di mana Anda mengalikan matriks penting karena, tidak seperti mengalikan dua nilai skalar, perkalian matriks tidak komutatif. Mengalikan matriks dalam urutan yang berlawanan memiliki efek visual menerjemahkan pelukis terbang ke posisi ruang dunianya, dan kemudian memutarnya di sekitar asal dunia.

Apa pun jenis matriks yang Anda buat, ingat aturan kiri ke kanan untuk memastikan bahwa Anda mencapai efek yang diharapkan.

Topik terkait

Transformasi