変換の行列表現

m×n の行列は、m 個の行と n 個の列に配置された一連の数値です。 次の図は、いくつかの行列を示したものです。

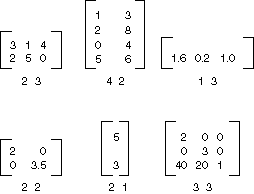
個々の要素を追加することにより、同じサイズの 2 つの行列を加算できます。 次の図は、行列の加算の例を 2 つ示したものです。

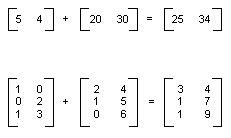
m×n の行列は m×p の行列で乗算でき、その結果は m×p の行列になります。 1 つ目の行列の列数は、2 つ目の行列の行数と同じである必要があります。 たとえば、4×2 の行列を 2×3 の行列で乗算すると、4×3 の行列が生成されます。

平面内の点と行列の行と列は、ベクターと考えることができます。 たとえば、(2, 5) は 2 つのコンポーネントを持つベクターで、(3, 7, 1) は 3 つのコンポーネントを持つベクターです。 2 つのベクターのドット積は、次のように定義されます。

(a, b) • (c, d) = ac + bd

(a, b, c) • (d, e, f) = ad + be + cf

たとえば、(2, 3) と (5, 4) のドット積は (2)(5) + (3)(4) = 22 です。 (2, 5, 1) と (4, 3, 1) のドット積は、(2) (4) + (5) (3) + (1) (1) = 24 です。 2 つのベクターのドット積は、別のベクターではなく、数値であることに注意してください。 また、ドット積を計算することができるのは、2 つのベクターのコンポーネント数が同じ場合に限られます。

A(i, j) が、ith 行と jth 列にある行列 A のエントリだとしましょう。 たとえば、A(3, 2) は 3 行目と 2列目にある行列 A のエントリです。 A、B、および C が行列で、AB = C であるとすると、C のエントリは次のように計算されます。

C(i, j) = (A の i 行) • (B の j 列)

次の図は、行列の乗算の例をいくつか示したものです。

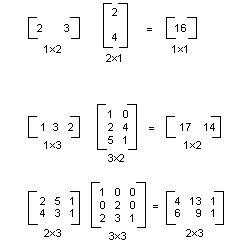
平面内の点が 1×2 の行列であると考えると、それを 2×2 の行列で乗算することで、その点を変換することができます。 次の図は、点 (2, 1) に適用されたいくつかの変換を示したものです。

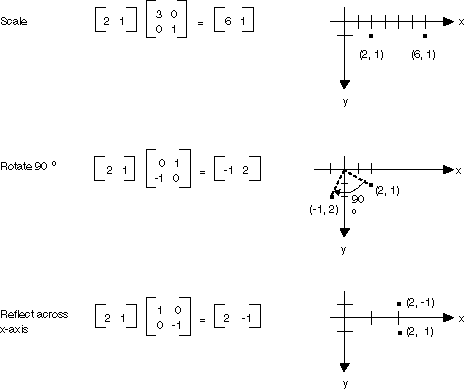
前の図に示されている変換はすべて、線形変換です。 平行移動などの特定の変換は線形ではなく、2×2 の行列による乗算として表すことはできません。 たとえば、点 (2, 1) で開始し、それを 90 度回転し、x 方向に 3 単位平行移動し、y 方向に 4 単位平行移動したいとします。 これを行うには、行列の乗算を使用し、その後に行列の加算を使用します。

線形変換 (2×2 の行列による乗算) の後に平行移動 (1×2 の行列の加算) を行う操作は、アフィン変換と呼ばれます。 1 組の行列 (線形部用と平行移動用) にアフィン変換を格納する代わりに、変換全体を 3×3 の行列に格納することもできます。 これを行うには、ダミーである 3 つ目の座標を使い、平面上の点を 1×3 の行列に格納する必要があります。 通常は、3 つ目の座標をすべて 1 に設定するという方法が使用されます。 たとえば、点 (2, 1) は、行列 [2 1 1] によって表されます。 次の図は、3×3 の行列による乗算として表されたアフィン変換 (90 度回転、x 方向に 3 単位平行移動、y 方向に 4 単位平行移動) を示したものです。

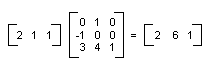
上記の例では、点 (2, 1) が点 (2, 6) にマップされています。 3×3 の行列の 3 列目の数値が、0、0、1 であることに注意してください。 これは、アフィン変換の 3×3 の行列において、常に当てはまります。 重要なのは、列 1 と列 2 の 6 つの数値です。 行列の左上の 2×2 の部分は変換の線形部分を表し、3 行目の最初の 2 つのエントリは平行移動を表します。

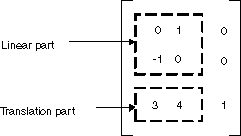
GDI+ では、アフィン変換を Matrix オブジェクトに格納できます。 アフィン変換を表す行列の 3 列目は常に (0, 0, 1) となるので、Matrix オブジェクトを構築する際には、最初の 2 列 に 6 つの数値のみを指定します。 ステートメント Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) を実行すると、上記の図に示されている行列が構築されます。

複合変換

複合変換とは、変換を順番に実行していく、変換のシーケンスのことです。 次の一覧に示す行列と変換について考えてみましょう。

Matrix	変換
行列 A	90 度回転
行列 B	x 方向に 2 倍に拡大
行列 C	y 方向に 3 単位平行移動

行列 [2 1 1] で表される点 (2, 1) で開始し、A 、B、C の順番で乗算すると、点 (2, 1) に対し、上記の順序で 3 つの変換が実行されます。

[2 1 1]ABC = [-2 5 1]

複合変換の 3 つの部分を 3 つの独立した行列に格納する代わりに、A、B、C を乗算して、複合変換全体を格納した 1 つの 3×3 行列を取得することもできます。 ABC = D とした場合、点を D で乗算した結果は、A、B、C の順に乗算した結果と同じになります。

[2 1 1]D = [-2 5 1]

次の図は、A、B、C、D の行列を示したものです。

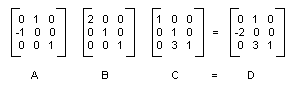
複合変換の行列は、個々の変換行列を乗算することで形成できます。つまり、1 つの Matrix オブジェクトには、アフィン変換の任意のシーケンスを格納することができます。

注意事項

複合変換では、順序が重要となります。 通常、回転、拡大縮小、平行移動という順序での操作は、スケーリング、回転、平行移動という順序での操作でと同じではありません。 同様に、行列の乗算においても順序が重要となります。 通常、ABC は BAC と同じではありません。

Matrix クラスには、複合変換を構築するためのメソッドがいくつか用意されています (Multiply、Rotate、RotateAt、Scale、Shear、および Translate)。 次の例では、最初に 30 度回転させた後、y 方向へ 2 倍に拡大し、x 方向に 5 単位平行移動する複合変換の行列を作成しています。

Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);

Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)

以下の図は、この行列を示したものです。

関連項目

• 座標系と変換
• マネージド GDI+ での変換の使用