Оптимизация моделей с помощью градиентного спуска

  • 6 мин

Мы рассмотрели, как функции потерь оценивают работу модели с помощью данных. Оптимизатор является заключительной частью головоломки.

Роль оптимизатора заключается в том, чтобы изменить модель таким образом, чтобы повысить его производительность. Это изменение выполняется путем проверки выходных данных модели и затрат и предложения новых параметров для модели.

Например, в нашем сценарии для фермерского хозяйства линейная модель имеет два параметра: пересечение линии и наклон линии. Если перехват линии неправильно, модель недооценивает или переоценивает температуры в среднем. Если наклон установлен неправильно, модель не сможет продемонстрировать, как изменились температуры по сравнению с пятидесятыми. Оптимизатор меняет эти два параметра, чтобы они давали оптимальный результат при моделировании температуры.

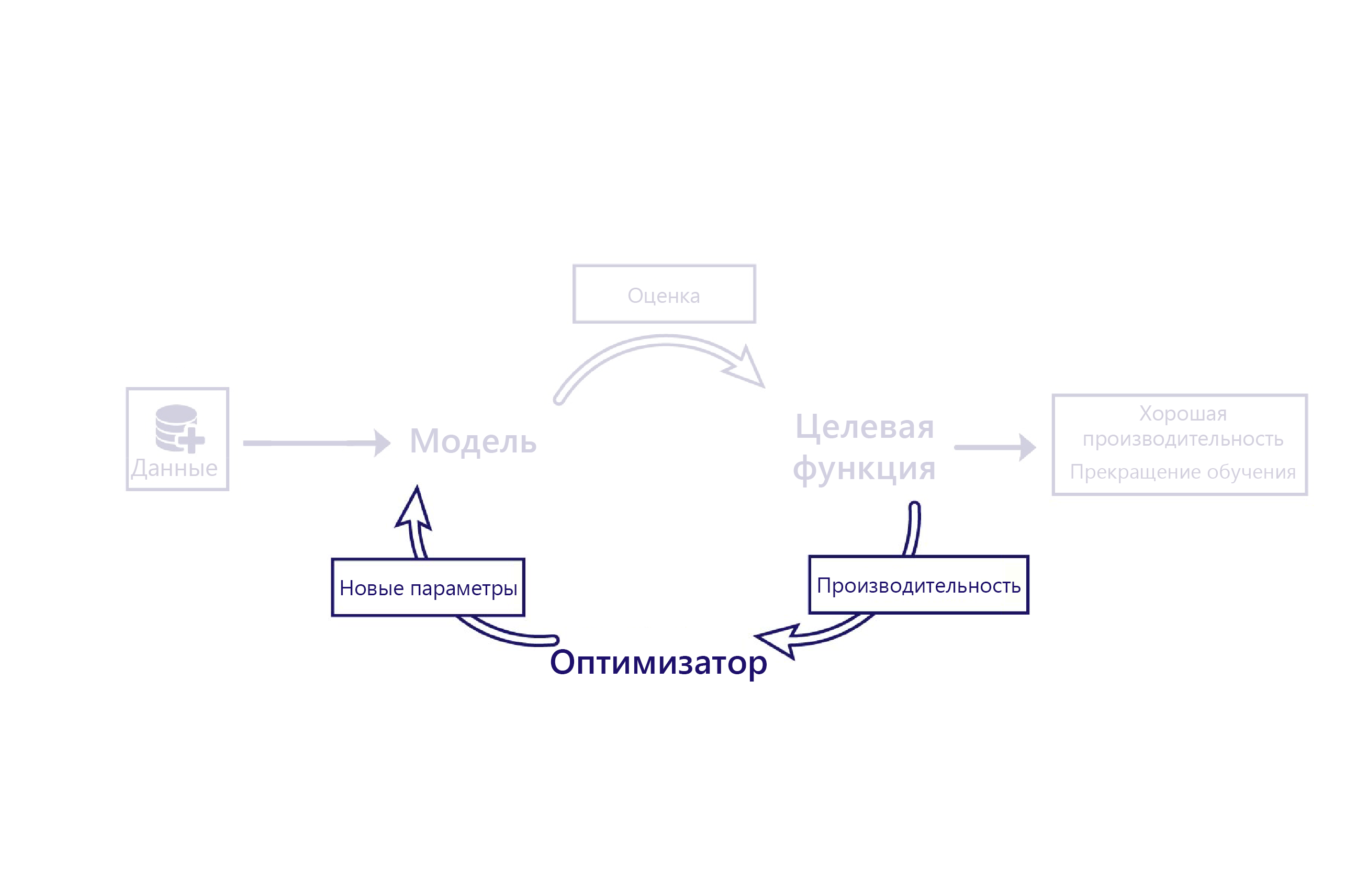
Diagram that shows the optimizer part of the machine-learning lifecycle.

Градиентный спуск

Сегодня наиболее распространенный алгоритм оптимизации — градиентный спуск. Существует несколько вариантов этого алгоритма, но все они используют одни и те же основные понятия.

Градиентный спуск использует вычисления для оценки того, как изменение каждого параметра изменяет стоимость. Например, можно спрогнозировать увеличение параметра, чтобы снизить потери.

Градиентный спуск назван так потому, что он вычисляет градиент (наклон) соотношения между каждым параметром модели и потерями. После этого параметры меняются, чтобы сместить наклон вниз.

Это простой и мощный алгоритм, который, однако, не гарантирует нахождение оптимальных параметров модели для минимизации потерь. Два основных источника ошибок — это локальный минимум и нестабильность.

Локальный минимум

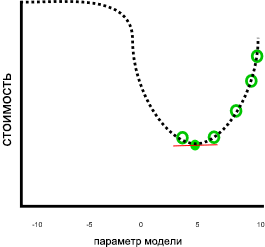
В предыдущем примере результат выглядел хорошо, если предположить, что потери продолжат расти, когда параметр меньше 0 или больше 10:

Plot of cost versus model parameter, with a minima for cost when the model parameter is five.

Это задание не было бы так велико, если параметры меньше нуля или больше 10 привели бы к снижению затрат, как на этом изображении:

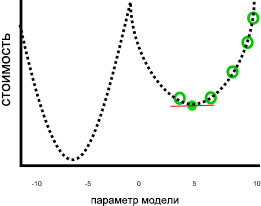
Plot of cost versus model parameter, with a local minima for cost when the model parameter is five but a lower cost when the model parameter is at negative six.

На предыдущем графе значение параметра отрицательного семи было бы лучшим решением, чем пять, так как оно имеет более низкую стоимость. Поскольку для метода градиентного спуска заранее не известна взаимосвязь между всеми параметрами и потерями, представленная в виде пунктирной линии, Поэтому он подвержен поиску локальной минимы: оценки параметров, которые не являются лучшим решением, но градиент равен нулю.

Нестабильность

Еще одна проблема заключается в том, что градиентный спуск иногда демонстрирует нестабильность. Такая неустойчивость обычно возникает, когда размер шага или скорость обучения (величина, на которую каждый параметр корректируется при каждой итерации) слишком велика. Тогда параметры меняются слишком сильно на каждом шаге, и модель фактически ухудшается с каждой итерацией:

Plot of cost versus model parameter, which shows cost moving in large steps with minimal decrease in cost.

Наличие более медленной скорости обучения может решить эту проблему, но может также привести к проблемам. Во-первых, более медленная скорость может означать, что обучение займет много времени, так как потребуется больше этапов. Во-вторых, выполнение меньших шагов делает его более вероятным, что обучение поселится на локальной миниме:

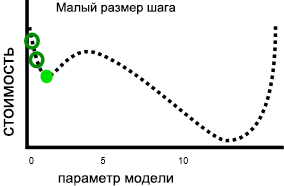
Plot of cost versus model parameter, showing small movements in cost.

В отличие от этого более быстрое обучение позволяет избежать попадания в локальный минимум, так как более большие этапы могут пропустить локальный минимум.

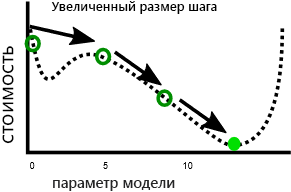
Plot of cost versus model parameter, with regular movements in cost until a minima is reached.

Как мы увидим в следующем упражнении, существует оптимальный размер шага для каждой проблемы. Для поиска такого оптимального размера часто необходимо провести эксперименты.