Векторы, вершины и кватернионы
В Direct3D вершины описывают положение и ориентацию. Каждая вершина в примитиве описывается вектором, который сообщает ее положение, цвет, координаты текстуры, и вектором нормали, который позволяет узнать ее ориентацию.
Кватернионы добавляют четвертый элемент к значениям [x, y, z], которые определяют трехкомпонентный вектор. Кватернионы представляют собой альтернативу матричным методам, обычно используемым для 3D-вращения. Кватернион представляет ось в 3D-пространстве и поворот вокруг этой оси. Например, кватернион может представлять ось (1,1,2) и поворот на 1 радиан. Кватернионы содержат полезную информацию, однако их истинная ценность заключается в двух операциях, которые можно выполнять над ними: композиции и интерполяции.
Выполнение композиции над кватернионами аналогично их объединению. Записывается композиция двух кватернионов так, как показано на следующем рисунке.
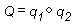
Композиция двух кватернионов, примененных к геометрии, означает "повернуть геометрию вокруг оси путем поворота, а затем повернуть ее вокруг оси' путем поворота₁". В этом случае Q представляет поворот вокруг одной оси, который является результатом применения q₁ к геометрии.
С помощью интерполяции кватернионов приложение может рассчитать плавный и рациональный путь от одной оси и ориентации к другой. Таким образом, интерполяция между q₁ и q₂ — это простой способ анимировать движение от одной ориентации к другой.
При совместном использовании композиция и интерполяция дают возможность без труда манипулировать геометрией так, что манипуляции будут казаться сложными. Например, предположим, что у вас есть геометрия, которую вы хотите повернуть для придания ей определенной ориентации. Вам известно, что нужно повернуть ее на r₂ градусов вокруг оси₂, а затем на r₁ градусов вокруг оси₁, однако окончательный кватернион вам не известен. Используя композицию, вы можете объединить два поворота применительно к геометрии и получить один кватернион, который будет представлять собой результат. Затем можно выполнить интерполяцию из исходного кватерниона в составной для получения плавного перехода от одного к другому.
Связанные темы
Обратная связь
Ожидается в ближайшее время: в течение 2024 года мы постепенно откажемся от GitHub Issues как механизма обратной связи для контента и заменим его новой системой обратной связи. Дополнительные сведения см. в разделе https://aka.ms/ContentUserFeedback.
Отправить и просмотреть отзыв по