Fastslå den optimale kombination af overlappende rabatter

Denne artikel beskriver, hvordan du kan fastslå den optimale kombination af overlappende rabatter i Microsoft Dynamics 365 Commerce.

Når rabatter overlapper hinanden, skal du bestemme den kombination af overlappende rabatter, der resulterer i den laveste samlede transaktion eller den højeste samlede rabat. Når rabatbeløbet afhænger af prisen på de produkter, der købes, f.eks. i den almindelige detailrabat (BOGO) "køb én, og få én X procent i rabat" (BOGO), bliver denne proces et problem med optimering af kombinationer.

Denne artikel gælder for Microsoft Dynamics AX 2012 R3 med KB 3105973 (udgivet 2. november 2015) eller nyere og for Dynamics 365 Commerce. For hurtigt at kunne bestemme den kombination af overlappende rabatter, der skal anvendes, har vi introduceret en metode til anvendelse af overlappende rabatter. Vi kalder denne nye metode rangordning af marginal værdi. I metoden rangordning af marginal værdi beregnes en værdi for hver overlappende rabat ved hjælp af rabatværdien for de delte produkter. De overlappende rabatter anvendes derefter fra den højeste relative værdi til den laveste relative værdi. Se afsnittet Metoden Rangordning af marginal værdi senere i denne artikel for at få oplysninger om den nye metode. Rangordning af marginal værdi bruges ikke, når rabatbeløbene for et produkt ikke er berørt af et andet produkt i transaktionen. Denne metode bruges f.eks. ikke til to enkle rabatter eller til en enkel rabat og mængderabat for et enkelt produkt.

Rabateksempler

Du kan oprette et ubegrænset antal rabatter på et fælles sæt produkter. Men fordi der ikke er nogen grænse, kan der opstå problemer med ydeevnen, når du forsøger at beregne de rabatter, der skal bruges på de forskellige produkter. Følgende eksempler illustrerer problemet mere detaljeret. Vi starter med to produkter og to overlappende rabatter i eksempel 1. Derefter viser vi i eksempel 2, hvordan problemet udvikles, når der tilføjes flere produkter.

Eksempel 1: To produkter og to rabatter

I dette eksempel er to produkter nødvendige for at kunne opnå hver rabat, og rabatter kan ikke kombineres. Rabatterne i dette eksempel er rabatter af typen bedste pris. Begge produkter opfylder betingelserne for begge rabatter. Her er de to rabatter.

For to tilfældige produkter afhænger den bedste af disse to rabatter af priserne på de to produkter. Når prisen på begge produkter er ens eller næsten ens, er rabat 1 den bedste. Når prisen på én vare er betydeligt mindre end prisen på det andet produkt, er rabatten 2 bedre. Her er den matematiske regel for evaluering af disse to rabatter mod hinanden.

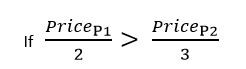
Bemærk!

Når prisen på produkt 1 er lig med to tredjedele af prisen på produkt 2, er de to rabatter lig hinanden. I dette eksempel varierer effektive rabatprocent for rabat 1 f.eks. fra et par procent (når priserne på de to produkter er langt fra hinanden) til maksimalt 25 procent (når de to produkter har den samme pris). Effektiv rabatprocent for rabat 2 er fast. Den er altid 20 procent. Da den effektive rabatprocent for rabat 1 har et interval, der kan være større eller mindre end rabat 2, afhænger den bedste rabat af priserne på de to produkter, der skal gives rabat på. I dette eksempel udføres beregningen hurtigt, fordi der kun anvendes to rabatter på kun to produkter. Der er kun to mulige kombinationer: én anvendelse af rabat 1 eller én anvendelse af rabat 2. Der er ingen kombinationsmuligheder, der skal beregnes. Værdien af hver rabat beregnes ved hjælp af begge produkter, og den bedste rabat bruges.

Eksempel 2: Fire produkter og to rabatter

Derefter skal bruge vi fire produkter og de samme to rabatter. Alle fire produkter opfylder betingelserne for begge rabatter. Der er tolv mulige kombinationer. I sidste ende anvendes to rabatter på transaktionen i en af tre kombinationer: to anvendelser af rabat 1, to programmer af rabat 2 eller en anvendelse af rabat 1 og en anvendelse af rabat 2. For at illustrere de mulige kombinationer ser vi nærmere på to forskellige sæt af fire produkter, der har forskellige priser:

• Alle fire produkter har den samme pris, $15,00. I dette tilfælde er den bedste rabatkombination to anvendelser af rabat 1. To produkter vil være til fuld pris, og to vil være med 50 procent rabat. Totalbeløbet med rabat for transaktionen er $45 (15 + 15 + 7,50 + 7,50), hvilket er $15 (25 procent) i rabat fra totalprisen uden rabat på $60. Rabat 2 er kun $12 (20 procent).
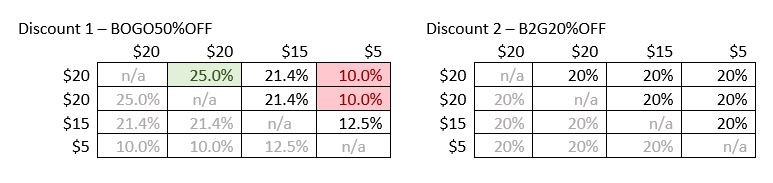
• To produkter koster $20 pr. stk., ét produkt koster $15, og et produkt koster $5. I dette tilfælde er den bedste rabatkombination én anvendelse af rabat 2 og én anvendelse af rabat 1. Nedenstående tabeller viser rabatterne.

For at læse tabellerne, skal du bruge et produkt fra en række og ét produkt fra en kolonne. I tabellen til rabat 1 får du f.eks. $10 i rabat, når du kombinerer de to produkter til $20. I tabellen til rabat 2 får du $4 i rabat, når du kombinerer produktet til $15 og produktet til $5.

Først skal vi finde den største rabat, der er tilgængelig for to vilkårlige produkter ved hjælp af begge rabatter. De to tabeller vises rabatbeløbet for alle kombinationer af de to produkter. De nedtonede dele af tabellerne repræsenterer enten tilfælde, hvor et produkt er parret med sig selv, hvilket vi ikke kan gøre, eller omvendt parring af to produkter, der giver det samme rabatbeløb og kan ignoreres. Ved at kigge på tabellerne kan du se, at rabat 1 for de to varer til $20 er den største rabat, der er tilgængelig for begge rabatter på alle fire produkter. (Denne rabat er fremhævet med grønt i den første tabel.) Det efterlader kun $15 produktet og $5 produktet. Ved at kigge på de to tabeller igen, kan du se, at for disse to produkter giver rabat 1 en rabat på $2,50, hvorimod rabat 2 giver en rabat på $4. Derfor vælger vi rabat 2. Den totale rabat er $14. For at gøre det nemmere at visualisere denne diskussion, er her to yderligere tabeller, der vises den effektive rabatprocent for alle mulige kombinationer af to produkter for både rabat 1 og rabat 2. Kun halvdelen oversigten over kombinationer er inkluderet, fordi den rækkefølge, hvori de to produkter er anbragt, ikke har nogen betydning. Den højeste effektive rabat (25 procent) er fremhævet med grønt og den laveste effektive rabat (10 procent) er fremhævet med rødt.

Bemærk!

Når priser varierer, og to eller flere rabatter konkurrerer, er den eneste måde til at sikre den bedste kombination af rabatter at evaluere begge rabatter og sammenligne dem.

Antal mulige kombinationer i alt

Dette afsnit fortsætter med eksemplet fra den forrige sektion. Vi vil tilføje flere produkter og en anden rabat og se, hvor mange kombinationer der skal beregnes og sammenlignes. Nedenstående tabel viser antallet af mulige rabatkombinationer, når produktantallet øges. I tabel vises, hvad der sker, både når der er to overlappende rabatter, som i forrige eksempel, og når der er tre overlappende rabatter. Antallet af mulige rabatkombinationer, der skal evalueres, overstiger hurtigt, hvad selv en hurtig computer kan beregne og sammenligne hurtigt nok, til at det er acceptabelt for detailtransaktioner.

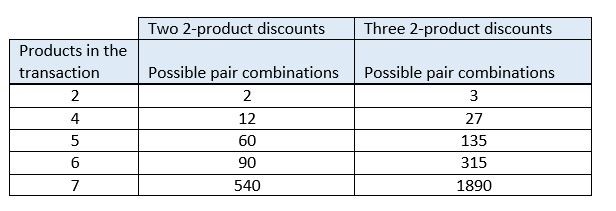
Når der anvendes større mængder eller flere overlappende rabatter, når det samlede antal mulige rabatkombinationer hurtigt op i millioner eller endda milliarder, og den tid, der kræves for at vurdere og vælge den bedste mulige kombination, bliver hurtigt mærkbar. Der skal foretages nogle optimeringer i prisprogrammet for at reducere det samlede antal kombinationer, der skal evalueres. Men fordi antallet af overlappende rabatter og mængderne i en transaktion ikke er begrænset, skal et stort antal kombinationer altid evalueres, når der er overlappende rabatter. Det er dette problem, som metoden rangordning af marginal værdi løser.

Metoden Rangordning af marginal værdi

Til at løse problemet med et eksponentielt stigende antal kombinationer, der skal evalueres, findes der en optimering, der beregner værdien pr. delt produkt for hver rabat på det sæt af produkter, hvor der kan anvendes to eller flere rabatter. Vi kalder denne værdi den marginale værdi af rabatten for de delte produkter. Den marginale værdi er den gennemsnitlige stigning pr. produkt stigning i det samlede rabatbeløb, når de delte produkter er inkluderet i hver rabat. Den marginale værdi beregnes ved at tage det samlede rabatbeløb (D_Total) og fratrække rabatbeløbet uden delte produkter (D_{Minus Shared}) og dividere forskellen med antallet af delte produkter (Items_Shared).

Når den marginale værdi af hver rabat på et delt sæt produkter er beregnet, anvendes rabatterne på de delte produkter i rækkefølge, udtømmende, fra højeste marginale værdi til laveste marginale værdi. I denne metode sammenlignes alle resterende rabatmuligheder ikke hver gang, når der anvendes en enkelt forekomst af en rabat. I stedet sammenlignes de overlappende rabatter én gang og anvendes derefter i rækkefølge. Der foretages ingen yderligere sammenligninger. Beregningen af rangordning af marginal værdi udløses automatisk, når antallet af mulige kombinationer i alt overstiger en foruddefineret grænse. Den acceptable tid til at beregne den samlede rabat varierer på tværs af detailbrancher. Men generelt ligger denne tid dog i intervallet fra nogle tiendedele af millisekunder til et sekund.