Drawing Fractal Trees - Part 3
The Application Itself
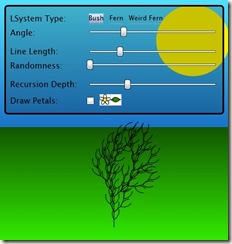
Firstly, here's what we're aiming towards:
Live demo: Click to view live.
Download the code:
Screenshot:
Writing The Application
Now, when I originally wrote the bones of the app it was very simple; everything fit in the single Page.xaml.cs file; there's actually very little to it. Since then I've expanded it to cater for all sorts of UI niceties and expansion opportunities, so it's a little bigger (and that's what's in the ZIP above). I'll concentrate on the basics for the purposes of the blog post; you can download the full source and inspect the complexities.
Step 1: Creating the Final Command Set
This step involves taking the Axiom and a set of rules, and using it to generate a final set of drawing commands/operations. The method below is in a class called LSystem, which is also where the axiom and rules are stored:
1: public string FinalCommandSet(int depth)
2: {
3: string res = Axiom;
4: for (int i = 1; i <= depth; i++)
5: {
6: foreach (LSystemRule rule in Rules)
7: {
8: res = res.Replace(rule.From, rule.To);
9: }
10: }
11:
12: return res;
13: }
Given the "depth" of recursion, we just loop through the latest string we have and apply all the rules at each step, starting with the axiom.
Now that we have this string, we need to walk through it and draw the final result.
Step 2: The Recursive Drawing Algorithm
1: int DrawSegment(Canvas uiRoot, string commandString, int stringPos,
2: Point curPos, double curAngle, double curLength)
3: {
4: Random rnd = new Random();
5: int i=stringPos;
6: while ( i < commandString.Length )
7: {
8: char c = commandString[i];
9: switch (c)
10: {
11: case '[':
12: i = DrawSegment( uiRoot, commandString, i+1, curPos,
13: curAngle, curLength );
14: break;
15:
16: case ']':
17: return i;
18:
19: case 'F':
20: Point newPos = FromAngleAndMagnitude(curPos, curAngle,
21: curLength + rnd.Next(this.Randomness/3));
22: DrawLine( uiRoot, curPos, newPos );
23: curPos = newPos;
24: break;
25:
26: case 'P':
27: if ( this.DrawPetals && (rnd.Next(100) < 90) )
28: DrawPetal(uiRoot, this.Petal, curPos, curAngle);
29: break;
30:
31: case '-':
32: curAngle -= this.Angle + rnd.Next(this.Randomness);
33: break;
34:
35: case '+':
36: curAngle += this.Angle + rnd.Next(this.Randomness);
37: break;
38: }
39: i++;
40: }
41:
42: return i;
43: }
First thing to note here is that the function is meant to be called recursively. The cases for '[' and ']' (lines 11 and 16) deal with that.
Next up, notice the overall loop; it's pretty much: "Step through each character of the string, act on that character, update our current pen settings (angle/position) as you go, and then move onto the next character."
Notice also that the function returns the final position in the string (i)that it ended up on; this is so that when you call it recursively, it reads as far as it can, then tells the caller where to continue from (see line 12).
At each call to the function, we pass in these args:
| uiRoot | The canvas to which we'll be adding any drawn lines. This is the same through all recursive calls. |
| commandString | The original/total string of commands. Stays the same through all calls. |
| stringPos | The current position in the command string; this changes through each recursive call. |
| curPos | The current position of the "pen" on the canvas; starts at the tree's origin, and changes with invocation of 'F'. |
| curAngle | The current angle/heading of the "pen" on the canvas; starts at 90 degrees, and changes with invocations of '+'/'-'. |
| curLength | The current length of a line when drawing with 'F'. This usually remains constant, but I added it in to allow for some funkier fractals that shrink with each recursion. |
Step 3: Drawing a Line
Finally, drawing a single line on the canvas is a matter of adding a Line shape to the canvas's Children member (slow, but simple). However, we only know the current location, the direction of the line, and the length. We need to convert this to a Start/End set of points.
A little trig:
1: private Point FromAngleAndMagnitude(Point origin,
2: double angle, double magnitude)
3: {
4: double radians = DegreesToRadians(angle);
5: return new Point(
6: (int) (magnitude * Math.Cos(radians)) + origin.X,
7: (int) (magnitude * -Math.Sin(radians)) + origin.Y
8: );
9: }
And that's pretty much it. Everything else is window dressing!
Further Reading
- Here's what happens when you take this technique just a little further: https://www.speedtree.com/gallery/
- Here's more info about the topic in general: https://vterrain.org/Plants/
- Here's info about using fractals to generate whole scenes (not just plants): https://vterrain.org/
Avi