7. Workflows – A Monad alias
Monads are one of the most complex concept to apprehend I encountered while learning functional programming, and unfortunately, like many developers I probably use them without understanding all the possibilities they offer. Before talking about what are Monads, it is interesting to understand where they come from. Monads come from Math, and are used as far as I know by two programming Haskell and F#.
Haskell designers philosophy was to create a pure functional programming language: a language without side effects. However there are side effects that you cannot avoid: The first unavoidable type of side effects coming to mind is IOs. Indeed if your functions have to, given the same input always return the same output, it would be impossible to represent some functions such as the one which gets a line typed on the keyboard by the user and returns it as a string. Interactions with the real world generate side effects.
In order to avoid creating an unusable language Haskell designers looked for a way to separate side effects code from the rest of the code, in way that pure and impure code won’t mix, if you introduce an impure function in a pure function the code is tainted as being impure. That’s where Monads come into play.
Monads represent a really generic powerful concept, which has a lot of other usages, as you will see F# don’t even use Monads for IO.
What are Monads?
Wikipedia:
“In functional programming , a monad is a programming structure that represents computations . Monads are a kind of abstract data typeconstructor that encapsulate program logic instead of data in the domain model . A defined monad allows the programmer to chain actions together and build different pipelines that process data in various steps, in which each action is decorated with additional processing rules provided by the monad. For example, a sequence of arithmetic operations can be controlled to avoid division by zero in intermediate results. Programs written in functional style can make use of monads to structure procedures that include sequenced operations,[1][2] or to define some arbitrary control flows (like handling concurrency , continuations , side effects such as input/output and variable assignment , or exceptions ).
Formally, a monad is constructed by defining two operations (bind and return) and a type constructor M that must fulfill several properties to allow the correct composition of monadic functions (i.e. functions that use values from the monad as their arguments). The return operation takes a value from a plain type and puts it into a monadic container of type M. The bind operation performs the reverse process, extracting the original value from the container and passing it to the associated next function in the pipeline.
A programmer uses an existing monad by composing monadic functions to define a new data-processing pipeline. The monad acts as a framework , as it's a reusable behavior that decides the order in which the specific monadic functions in the pipeline are called, and manages all the undercover work required by the computation.[3] The bind and return operators interleaved in the pipeline will be executed after each monadic function returns control, and will take care of the particular aspects handled by the monad.
The name is taken from the mathematical monad construct in category theory , though the two concepts are not identical.”
This definition is quite big, and hard to understand, let’s highlight the important ideas:
1- A monad is a programming structure that represents computations
2- A defined monad allows the programmer to chain actions together
3- A monad is constructed by defining two operations (bind and return) and a type constructor M that must fulfill several properties to allow the correct composition of monadic functions
Better an example than precept
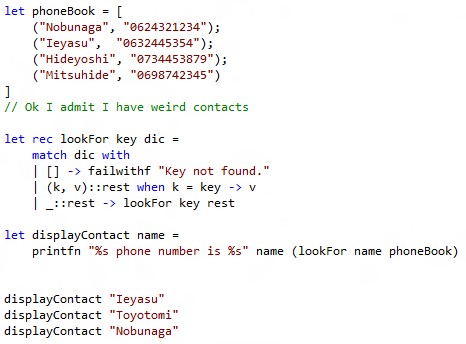
Let’s say you want to define a function to look for an element in a key value pair list given its key , this function could have the type: (‘a –> (‘a * ‘b) list –> ‘b) if an equality operator is defined for type ‘a.
In the following example the list of pairs is a phone book. It associates contact names with phone numbers. I want to get a phone number given a contact name:
About the contact names chosen in this example: In Warring States period, the whole Japan history might have changed on June 21, 1582, if Hideyoshi had a mobile phone. Due to simple a letter which didn’t come on time, the most powerful Japanese Daimyou, Oda Nobunaga died, killed by one of his men Mitsuhide who misunderstood his true intentions.
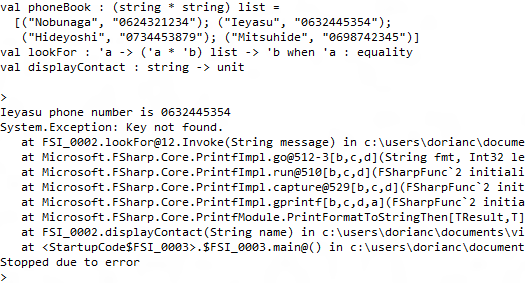
Our function lookFor works nice, however it has a quite heavy behavior when a key is not found, it throws an exception. In dynamic typed languages you could return some meaningful value such as a false boolean value if a key is not found. In typed languages such as C# you could use a null value, however you probably know that it has to be handled carefully, since if not some null reference exceptions may appear in your code, returned values need to be checked on each call. That’s why without exception C#, error handling and propagation would look pretty like C:
It is interesting to notice how with the indentation the code is going to the right, making it hard to read. I will talk about it later.
We wish our functions to be able to either return a valid result or a meaningful value to indicate our computation failed, if failed the status should be propagated skipping the next computing steps. And possibly avoiding the code overhead needed to achieve this propagation (which makes your code little by little indent to the right.)
Believe it or not, but Monads can help us here.
First, we are going to create a type to represent the fact a computation may or may not success in returning a value. And then update our lookFor function definition to use this type.
The maybe type is a generic type, when a function successes it will return Just value, and when it fails it will return Nothing:
Although more meaningful, we now have an equivalent to the return valid value or return null value pattern we showed in C#.
Note: There already is a type equivalent to Maybe<’a>, it is defined in the F# core library and called option<’a>.
Let say I want to create a function which given a phone book will check that all my friends contact are in it, and return their numbers. If one of my contact numbers is not in the phone book the whole function should tell me it failed. If you follow the cascading if pattern, you will get something like:
That’s bad right? We still have these redundant checks on the result values, and the code keeps moving to the right. We are going to try factorize this a little first :
We use here a pattern quite common in functional programming languages which consists in capturing continuations with closures (cf. my article on continuations). If you come from non functional language and worked with some asynchronous code, you may be familiar with the concept of callbacks which is similar.
Here we succeeded in factorizing the conditional (match) expressions by defining a check function. This function takes a Maybe value and a function representing a continuation, and according to the value it stops or continue the computation with the value wrapped by the Just constructor.
We are close from a Monad here, actually, if we generalize our code a little more it is one. Conceptually, we have a context, the type representing a possibility of failure, this context wraps a value, and thanks to a function, check in our example we are able to propagate this context through the different steps of our computation by extracting and wrapping back the value into the context. The function we use to wrap back the value into a context is in our specific case the Just type constructor.
If you remember one of the points we highlighted previously: “A monad is constructed by defining two operations (bind and return) and a type constructor M that must fulfill several properties to allow the correct composition of monadic functions”.
The check function we defined is the bind operation, while the Just constructor is our return operation:
Ok, I know, what you are thinking, I just renamed some functions. But it is important to clearly see those two operations. And by defining them we officially created our first Monad!
A Monad, is it only that???
No, no, don’t worry, there is more to come. The previous pattern I showed you may appear quite specific to my error handling problem, but actually it is really generic! So generic that the concept of Monads got its own syntax in Haskell and F#.
But, first I have to admit I lied to you, Monads aren’t called Monads in F#, they are called workflows, or computational expressions. And if you remember the second point we highlighted in the Monad definition, you can easily understand why: “A defined monad allows the programmer to chain actions together”. It is exactly what we did in our error handling example, we chained functions calls, in a way the failure context is managed and propagated between calls.
To define a Monad in F# and take advantage of a syntax I am going to show you, we need to make a builder type.
A builder is a .NET class that contains methods definitions for the bind and return operations, and possibly other operations related to F# monads. To correctly define this class we need at least to implement three methods Return(value), Bind(value, continuation) and Zero(). The Zero() method returns the default Monadic value. Once we have this class, we make a singleton instance from it.
This is the correct way to define a basic Monad in F#.
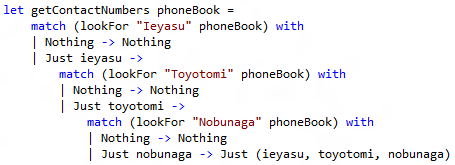
We can now enjoy a more friendly syntax to rewrite our getContactNumbers function.
Look how nice this code looks!
Our code which was moving to the right and was hardly readable is now really concise and clear. What happened here? We used our singleton instance, curly braces and the new let! and return keywords to improve the readability. Under the hood let! just calls our Monad Bind(…) operation, implicitly capturing the current continuation while the return keyword calls our Monad Return(…) method. If you are an imperative programmer it is really important to understand that the return keyword has strictly nothing to do with the return keyword you may encounter in C, C++, or C# for example: it won’t break the flow of a computation, it is just a way to wrap a value into the context expressed by the used Monad.
You already know a Monad…
I told you the monad concept, although strange at a first glance, is really powerful and generic. The proof is that if you read my previous article on Sequences, you already met and used Monads.
Indeed F# sequences are Monads! And in Haskell even list are monads. Why? Because if you think about it, list or sequences are just a context around values, and you may want to propagate this sequence context through computations while modifying the value(s) wrapped.
Here the yield keyword is a keyword strictly equivalent to the return keyword, it has been introduced to make the return keyword use in sequences more natural. If you know generators in languages such as Python or C#, you probably understand why.
Windows 8, coming soon…
As you probably know, Windows 8 is going to be released in a few weeks. If you already tried to look at how to develop Metro UI applications in C#, you probably encountered two new keywords (C# 5.0): The async, and await keywords.
WinRT the native library behind Metro, has been designed to use and force the use of an asynchronous model for parallelism. Parallelism is necessary to handle time consuming operations outside the UI thread, and then avoiding freezing the UI and degrade the user experience.
The main asynchronous model advantage is that it prevents most developers (95% of them?) to keep playing randomly with threads and synchronization object: This is indeed a fact, most developers don’t know how to correctly use parallelism and…
NON EXPERT DEVELOPER + THREADING + SIDE EFFECTS = CHAOS
You can replace chaos by:
- Deadlocks
- Inability to debug programs
- Program crashing once or twice a month without any reason
- Computer crashes
- Train accidents
- Aircraft crashes
- …
- End of the world?
And I wondering if it is not the reason why functional programming languages are recently coming back to the scene.
Indeedwe are in the era of parallelism: multicore processors / distributed computations and shared resources with cloud computing / web and communication (part of the IOs in a program increasing). Functional languages by discouraging side effects make parallelism safer, and ease its use with a lot of powerful concepts.
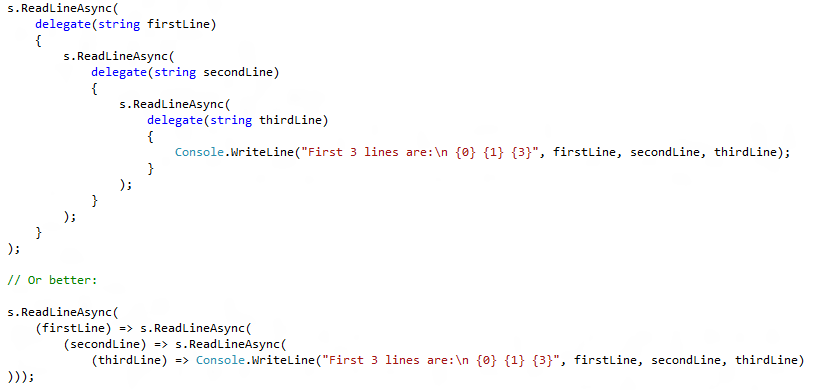
The main asynchronous model drawback is that it is not natural. Look at this C# example:
With all this code, I am just reading three lines from a stream through the use of an asynchronous method, and displaying them. Look how intuitive this code can be… And be happy without closures in C#, you couldn’t write it so easily.
Earlier when we were working on the path leading to Monads, I wrote something about the fact callbacks could be considered as a similar concept for continuations. Look at the code, it is moving to the right, and we are capturing continuations, the “which operation should be done next”. You guess it now, there is a Monad to deal with asynchronous operations.
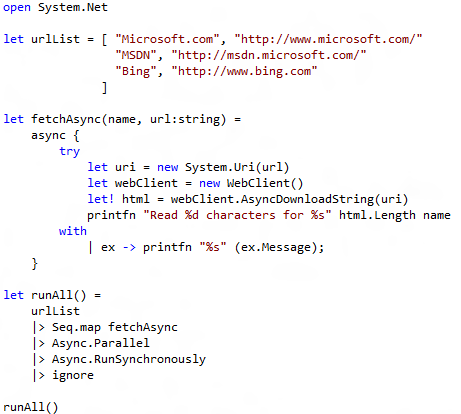
It is called async,in F# and you use it like this:
The use of let! here captures the current continuation and calls it with the result once the page is downloaded.
C# the next functional programming language?
Believe it or not, but after borrowing the concept of garbage collector (LISP), the OOP paradigm (LISP), closures, Linq, C# is now borrowing an other powerful concept from the functional programming world: Monads, more precisely the async particular monad.
WinRT designers made a choice, between allowing developers to use threads – should be read “Making children play with bazooka” – or make the move to a non natural programming model for imperative languages. To turn the asynchronous C# into something useable, they needed a powerful addition coming from the functional programming world.
But we still have a problem here… Among C# developers, who knows about Monads?
Who knows that the await keyword is a disguised bind operation capturing the current continuation within an async method ?
You could rightly argue it is irrelevant since what is important is to know how to use it. I would answer OS designers thought the same way when they introduced preemptive schedulers, and gave developers process/threading APIs.