Embracing Uncertainty – Probabilistic Inference
This is the second of a 2-part blog post by Chris Bishop, Distinguished Scientist at Microsoft Research. The first part is available here.
Last week we explored the key role played by probabilities in machine learning, and we saw some of the advantages of arranging for the outputs of a classifier to represent probabilities rather than decisions. In fact, nearly all of the classifiers in Azure ML can be used to generate probabilistic outputs. However, this represents only a glimpse of the many ways in which probabilistic methods can be used in ML. This week, we will explore some further benefits arising from a deeper use of probabilities as part of the training process.
The Curse of Over-Fitting
Traditionally, the parameters of a classifier are tuned by minimizing an error function which is defined using a set of labelled data. This is a computationally expensive process and constitutes the training phase of developing a ML solution. A major practical problem in this approach is that of over-fitting, whereby a trained model appears to give good results on the training data, but where its performance measured on independent validation data is significantly worse. We can think of over-fitting as arising from the fact that any practical training set is finite in size, and during training the parameters of the model become finely tuned to the noise on the individual data points in the training set.
Over-fitting can be controlled by a variety of measures, for example by limiting the number of free parameters in the model, by stopping the training procedure before the minimum training error is reached, or by adding regularization terms to the error function. In each case there is at least one hyper-parameter (the number of parameters, the stopping time, or the regularization coefficient) that must be set using validation data that is independent of the data used during training. More sophisticated models can involve multiple hyper-parameters, and typically many training runs are performed using different hyper-parameter values in order to select the model with the best performance on the validation data. This process is time-consuming for data scientists, and requires a lot of computational resources.
So is over-fitting a fundamental and unavoidable problem in ML? To find out we need to explore a broader role for probabilities.
Parameter Uncertainty
We saw last week how probabilities provide a consistent way to quantify uncertainty. The parameters of a ML model (for example the weights in a neural network) are quantities whose values we are uncertain about, and which can therefore be described using probabilities. The initial uncertainty in the parameters can be expressed as a broad prior distribution. We can then incorporate the training data, using an elegant piece of mathematics called Bayes’ theorem, to give a refined distribution representing the reduced uncertainty in the parameters. If we had an infinitely large training set then this uncertainty would go to zero. We would then have point values for the parameters, and this approach would become equivalent to standard error-function minimization.
For a finite data set, the problem of over-fitting, which arose because error-function minimization set the parameters to very specific values with zero uncertainty, has disappeared! Instead, the uncertainty in the weights provides an additional contribution to the uncertainty in the model predictions, over and above that due to noise on the target labels. If we have lots of parameters in the model and only a few training points, then there is a large uncertainty on the predictions. As we include more and more training data, the level of uncertainty on our predictions decreases, as we would intuitively expect.
Hierarchical Models
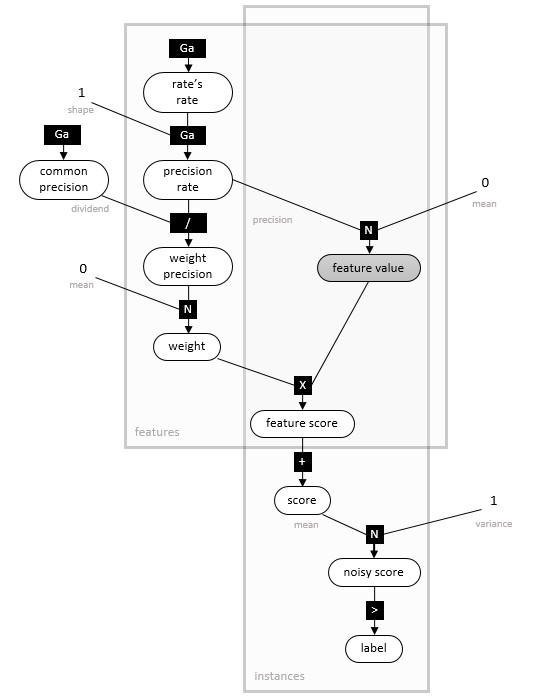
A natural question is how to set the hyper-parameters of the prior distribution. Because we are uncertain of their values they should themselves be described by probability distributions, leading – it seems – to an infinite hierarchy of probabilities. However, in a recent breakthrough by scientists at Microsoft Research it has been shown that only a finite hierarchy is required in practice, provided it is set up in the correct way (technically a mixture of Gamma-Gamma distributions). The result is a model that has no external hyper-parameters. Consequently, the model can be trained in a single pass, without over-fitting, and without needing pre-processing steps such as data re-scaling. The structure of such a model is illustrated for a simple two-class classifier known as the Bayes Point Machine, in the figure below:
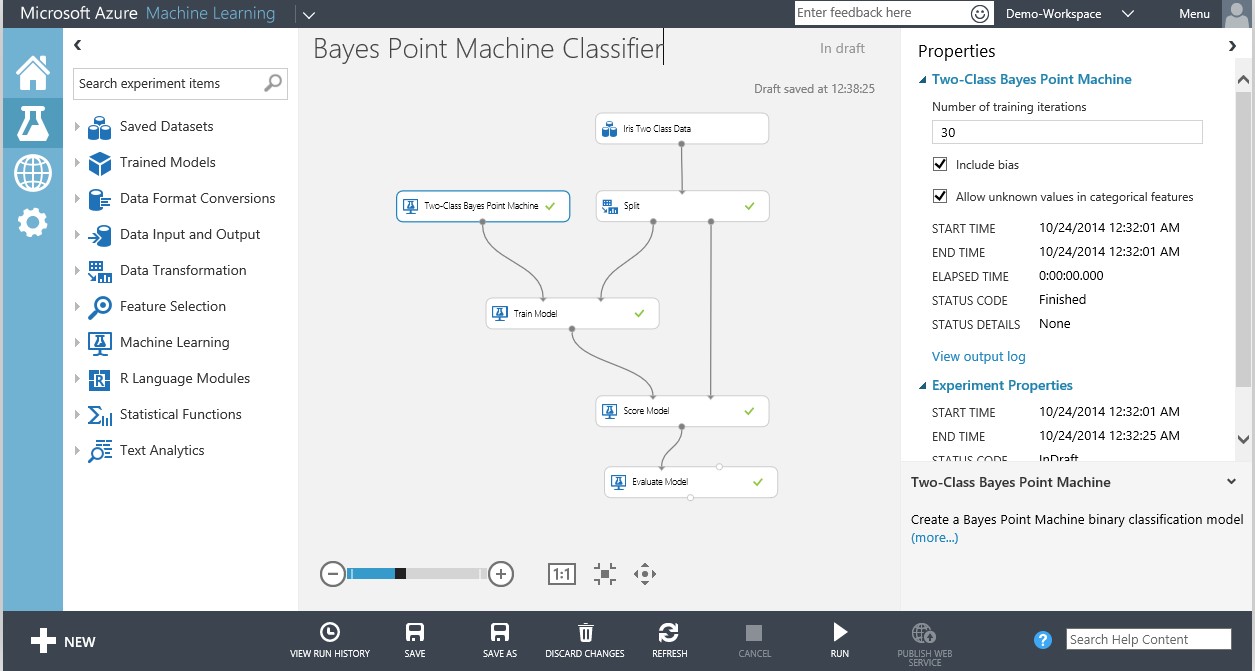
This diagram is an example of a factor graph which illustrates the variables in the model along with their probability distributions and inter-dependencies. Although the training of such a model using distributions is slightly more costly compared to the use of an optimization algorithm, the model only needs to be trained once, resulting in a significant overall saving in time and resources. The two-class Bayes Point Machines is available in Azure ML, and its use is illustrated in the following screen shot:
Towards Artificial Intelligence
So have we exhausted the possibilities of what can be achieved using probabilities in ML? Far from it – we have just scratched the surface. As the field of ML moves beyond simple prediction engines towards the ultimate goal of intelligent machines, rich probabilistic models will become increasingly vital in allowing machines to reason and learn about the world and to take actions in the face of uncertainty.
We must leave a more detailed discussion of this fascinating frontier of ML to a future article. Meanwhile, I encourage you to explore the world of probabilities further using the Bayes Point Machine in Azure ML.
Chris Bishop
Learn about my research