How to calculate barcode check-digit using T-SQL language
Editor's note: The following post was written by Data Platform MVP Sergio Govoni as part of our Technical Tuesday series. Mia Chang of the MVP Award Blog Technical Committee served as the technical reviewer for this piece.
In order to scale, it’s imperative that companies stay ahead of competition. So how can they identify, store, manage and deliver goods to customers efficiently? The answer is: Barcode! A barcode is the graphical representation of a sequence of numbers and other symbols. The representation is made by lines (bars) and spaces. A barcode typically consists of five parts - and one of these is the check character, also known as the check digit. Handwriting this is a hard work, and is also susceptible to legibility problems. Barcoding dramatically reduces human error, recognition errors and transcription errors.
This article explores the algorithm needed to calculate the check-digit of an UCC/EAN barcode. It compares two possible implementations of the algorithm to calculate the check character for an EAN13 barcode using T-SQL language for SQL Server.
UCC/EAN standard coding
The UCC/EAN standard coding requires that every (well-formed) code ends with a check-digit that will be used by barcode readers to interpret the code properly. The check-digit is a number between zero and nine and it is calculated according to the other digits in the code.
The calculation algorithm requires that every digit in the code is enumerated from right to left, is shown here.
After you have enumerated each digit of the given code, you need to do the following steps to determine the check character:
-
- Add up the digits in the even positions
- Multiply the result of the previous step by three
- Add up the digits in the odd positions
- Add up the results obtained in steps two and three
- Subtract the upper multiple of 10 from the result obtained in step four. For example, if the result of step four is 47, subtract 50 from 47, so the result is 3.
If the result of the four step is a multiple of ten, the check-digit will be equal to zero. Otherwise the check-digit will be the result of the fifth step.
Let’s implement the algorithm using T-SQL language
Suppose that your boss asked you to implement a T-SQL object, in an SQL Server database, that it is able to calculate the check-digit for a given EAN13 code. How can you translate the standard algorithm to T-SQL code?
One possible solution could be implemented by a user-defined scalar-valued function that receives an EAN13 code as input, and gives out the check-digit calculated for the given code. In reading the algorithm step-by-step, the most natural and obvious solution is implemented by the following T-SQL function.
CREATE FUNCTION dbo.udf_get_check_digit_ucc_ean13
(
@ACode AS VARCHAR(12)
)
RETURNS SMALLINT
AS BEGIN
/*
Author: Sergio Govoni
Notes: This function is able to calculate the check-digit of an EAN13 code
Version: 1.0
*/
DECLARE @tmpCode AS VARCHAR(12),
@tmpMulSup AS VARCHAR(8000),
@tmp AS VARCHAR(8000),
@i AS INT,
@j AS INT,
@z AS INT,
@SumDEven AS INT,
@SumDOdd AS INT,
@List AS VARCHAR(8000),
@tmpList AS VARCHAR(8000),
@CheckSum AS SMALLINT
SET @SumDEven = 0
SET @SumDOdd = 0
SET @List = ''
SET @tmpList = ''
SET @tmp = ''
SET @tmpCode = @ACode
/* 0. List builder */
SET @j = LEN(@tmpCode) + 1
SET @i = 1
WHILE (@i <= LEN(@tmpCode)) BEGIN SET @List = @List + '|' + LTRIM(RTRIM(STR(@j))) + ';' + SUBSTRING(@tmpCode, @i, 1) SET @j = (@j - 1) SET @i = (@i + 1) END /* 1. Add up the digits in even position */ SET @i = 1 SET @tmpList = @List WHILE (CHARINDEX('|', @tmpList) > 0)
BEGIN
SET @j = CHARINDEX('|', @tmpList)
SET @z = CHARINDEX(';', @tmpList)
IF (CAST(SUBSTRING(@tmpList, (@j + 1), (@z - (@j + 1))) AS INTEGER) % 2) = 0
BEGIN
SET @SumDEven = @SumDEven + CAST(SUBSTRING(@tmpList, (@z + 1), 1) AS INTEGER)
END
SET @tmpList = SUBSTRING(@tmpList, (@z + 2), LEN(@tmpList))
END
/* 2. Multiply the result of the previous step (the first step) to 3 (three) */
SET @SumDEven = (@SumDEven * 3)
/* 3. Add up the digits in the odd positions */
SET @i = 1
SET @tmpList = @List
WHILE (CHARINDEX('|', @tmpList) > 0)
BEGIN
SET @j = CHARINDEX('|', @tmpList)
SET @z = CHARINDEX(';', @tmpList)
IF (CAST(SUBSTRING(@tmpList, (@j + 1), (@z - (@j + 1))) AS INTEGER) % 2) <> 0
BEGIN
SET @SumDOdd = @SumDOdd + CAST(SUBSTRING(@tmpList, (@z + 1), 1) AS INTEGER)
END
SET @tmpList = SUBSTRING(@tmpList, (@z + 2), LEN(@tmpList))
END
/* 4. Add up the results obtained in steps two and three */
SET @CheckSum = (@SumDEven + @SumDOdd)
/* 5. Subtract the upper multiple of 10 from the result obtained in step four */
IF ((@CheckSum % 10) = 0)
BEGIN
/* If the result of the four step is a multiple of Ten (10), like
Twenty, Thirty, Forty and so on,
the check-digit will be equal to zero, otherwise the check-digit will be
the result of the fifth step
*/
SET @CheckSum = 0
END
ELSE BEGIN
SET @tmpMulSup = LTRIM(RTRIM(STR(@CheckSum)))
SET @i = 0
WHILE @i <= (LEN(@tmpMulSup) - 1)
BEGIN
SET @tmp = @tmp + SUBSTRING(@tmpMulSup, @i, 1)
IF (@i = LEN(@tmpMulSup) - 1)
BEGIN
SET @tmp = LTRIM(RTRIM(STR(CAST(@tmp AS INTEGER) + 1)))
SET @tmp = @tmp + '0'
END
SET @i = (@i + 1)
END
SET @CheckSum = CAST(@tmp AS INTEGER) - @CheckSum
END
RETURN @CheckSum
END;
This implementation of the algorithm to calculate check-digit works fine. If you try to calculate the check character for the sample barcode “801271210146” the function will return the number five, so, the check digit for the given barcode is five.
SELECT
[check-digit] = dbo.udf_get_check_digit_ucc_ean13('801271210146');
GO
If you compare the result of the function -five - with the check-digit calculated by the GS1 check digit calculator, we observe that they are equal. The result of GS1 check digit calculator is shown in the following picture.
[caption id="attachment_24015" align="alignnone" width="782"]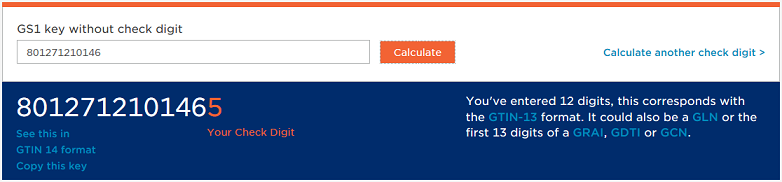 Picture: Check character for the barcode number “801271210146”[/caption]
Picture: Check character for the barcode number “801271210146”[/caption]
The first version of the function dbo.udf_get_check_digit_ucc_ean13 has been implemented with a row-by-row approach. But is it really the best solution? Let’s think outside the code. The code is just a tool. We have to try to find out the logical solution and then translate it into T-SQL commands.
Usually, one immediately begins by realizing the first solution that comes to mind, and solving all the problems that arise - performance problems are the first type of issue that one usually takes on. But let’s give up this approach and try to find the best algorithm (language-independent) that can solve the problem. This is called “set-based thinking”. In chatting with Joe Celko, I found a set-based solution to implement the check-digit algorithm.
Set-based thinking
With the following, you can find the 2.0 version of the function dbo.udf_get_check_digit_ucc_ean13.
CREATE FUNCTION dbo.udf_get_check_digit_ucc_ean13
(
@ACode AS VARCHAR(12)
)
RETURNS INTEGER
AS BEGIN
RETURN (10 - (3* CAST(SUBSTRING('0' + @ACode, 1, 1) AS INTEGER)
+ CAST(SUBSTRING('0' + @ACode, 2, 1) AS INTEGER)
+ 3* CAST(SUBSTRING('0' + @ACode, 3, 1) AS INTEGER)
+ CAST(SUBSTRING('0' + @ACode, 4, 1) AS INTEGER)
+ 3* CAST(SUBSTRING('0' + @ACode, 5, 1) AS INTEGER)
+ CAST(SUBSTRING('0' + @ACode, 6, 1) AS INTEGER)
+ 3* CAST(SUBSTRING('0' + @ACode, 7, 1) AS INTEGER)
+ CAST(SUBSTRING('0' + @ACode, 8, 1) AS INTEGER)
+ 3* CAST(SUBSTRING('0' + @ACode, 9, 1) AS INTEGER)
+ CAST(SUBSTRING('0' + @ACode, 10, 1) AS INTEGER)
+ 3* CAST(SUBSTRING('0' + @ACode, 11, 1) AS INTEGER)
+ CAST(SUBSTRING('0' + @ACode, 12, 1) AS INTEGER)
+ 3* CAST(SUBSTRING('0' + @ACode, 13, 1) AS INTEGER)
)%10
)%10
END;
Why is set-based thinking so difficult? Set-based thinking is difficult Because we usually think that data are stored in a specific order, fetch operations guarantee the orderly return of data portions, one portion at a time. Our mind sees data in these terms:
- In an orderly manner
- Manipulated in portions, one portion at a time
As the previous version, the 2.0 version of the function dbo.udf_get_check_digit_ucc_ean13 works properly, but it’s better because it uses a set-based approach instead of row-by-row ones. And it also works fine on Azure SQL Database.
Conclusion
Barcodes offer companies automatic product identification, extremely fast warehouse movement and very fast data recognition and implementation. This means that barcodes improve productivity, and help companies save time and money. For each barcode that is generated (independently from the type: EAN8, EAN12, EAN13, EAN14, GTIN and SSCC) one has to calculate the check-digit, in order to add it at the end of the barcode characters.
In this article, we learned how to implement the check digit algorithm with T-SQL language using a user-defined function, saved in a user or system database in a SQL Server instance. We optimized the first version of the function using set-based theory. The function dbo.udf_get_check_digit_ucc_ean13 can be used directly in a T-SQL statement to obtain the check character of a given barcode.
Enjoy working with the EAN13 check-digit calculator!
 Sergio Govoni has been a software developer for almost 20 years. He received a Computer Science degree from Italy State University in 2000. He’s since worked at Centro Software, which produces an international multi-company ERP on the Windows platform. At Centro Software, Sergio currently serves as Technical Lead and manages the architecture and mission-critical technical details on team projects. Based in Bologna, Italy, Sergio has been a Microsoft Data Platform MVP (SQL Server category) since 2010. Follow him on Twitter @segovoni.
Sergio Govoni has been a software developer for almost 20 years. He received a Computer Science degree from Italy State University in 2000. He’s since worked at Centro Software, which produces an international multi-company ERP on the Windows platform. At Centro Software, Sergio currently serves as Technical Lead and manages the architecture and mission-critical technical details on team projects. Based in Bologna, Italy, Sergio has been a Microsoft Data Platform MVP (SQL Server category) since 2010. Follow him on Twitter @segovoni.