Test Run
Using Combinations to Improve Your Software Test Case Generation
Dr. James McCaffrey
Code download available at:TestRun0407.exe(132 KB)
Contents
Combinations
A Combination Class
Calculating the Number of Combination Elements
Generating All Combination Elements
Conclusion
Testing has always been a vital part of the software development process, but three recent factors have caused it to take an even more central role. First, the introduction of the Microsoft® .NET environment has dramatically improved developers' ability to write custom test automation. Test programs that took weeks to create before the .NET Framework can now be written in just hours. Second, increasingly complex systems are being built that require more sophisticated testing. Finally, software security is no longer an afterthought of the development process; it is an absolute essential. It once was possible to push a product out the door without complete testing, but this is no longer a viable option. To help you meet today's testing challenges I will show you best practices, principles, and techniques of software testing right here in this column every few months.
This month I'll begin with the role of combinations in software testing. The ability to programmatically generate combinations gives you a powerful way to generate test case input. To see what I mean about combinations, suppose you are writing a poker program. Manually generating all possible five-card test inputs would not be pleasant. But with the code in this column you can do it in minutes:
string[] deck = new string[] { "Ac", "Ad", "Ah", "As", "Kc", (...) }; Combination c = new Combination(52,5); // 52 cards, 5 at a time string[] pokerHand = new string[5]; while (c != null) { pokerHand = c.ApplyTo(deck); PrintHand(pokerHand); c = c.Successor(); }
The number of test automation scenarios in which combinations are useful is astonishing once you learn to recognize them. As another example, suppose you are testing some system that accepts user input into a textbox that holds 10 characters. One input might be "ABCDEFGHIJ" and another might be "!@#$%^&*()". You want to know how many different test cases there are. Let's assume you've determined that the character input falls into 20 equivalence classes—categories that are equivalent as far as your system is concerned. One equivalence class might be uppercase A through Z and another equivalence class might be the digits 0 through 9.
Notice that you must select 10 characters and each character must come from one of 20 categories. So you have 20 items taken 10 at a time, or Choose(20,10)—a function I'll discuss a little later in this column. Note that I have simplified this scenario. In practice, you would also need to consider permutations of each combination along with boundary conditions and many other test concepts.
Here I will build a Combination class in C# and show you how to use combinations to improve your testing effort. I think you'll find that understanding and using combinations and their associated algorithms are valuable assets.
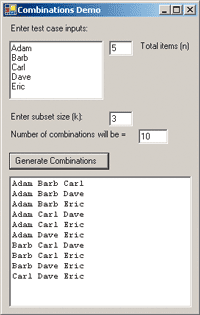
Figure 1** Combinations Demo **
The best way to show you where I'm headed is with a screen shot. Figure 1 is a screen of a Windows®-based application that demonstrates the use of combinations. As you can see, a combination of items is a subset of those items in which order does not matter. In this example I have five items—the names Adam, Barb, Carl, Dave, and Eric—and I am interested in combinations of size 3. There are 10 possible subsets of the 5 items taken 3 at a time:
{ Adam, Barb, Carl }, { Adam, Barb, Dave }, . . . { Carl, Dave, Eric }
Notice that since order doesn't matter I don't count a subset like { Carl, Barb, Adam } because I consider it the same as { Adam, Barb, Carl }. The example in Figure 1 also illustrates that in addition to generating combinations, I need the ability to compute how many combinations there are for a particular item set size and subset size.
A mathematical combination is a generalization of this idea of subsets. Instead of being a subset of arbitrary items, a mathematical combination of order n is a subset of the integers from 0 up to n-1. So the six elements of a mathematical combination of four items taken two at a time are:
{ 0, 1 }{ 1, 2 } { 0, 2 } { 1, 3 } { 0, 3 } { 2, 3 }
As I said, combinations are enormously useful in a surprising number of areas of software test automation, development, and management. While the mathematical concepts behind combinations are old and deep, I recently discovered that, in general, combinations are not well understood by software engineers, and that the majority of combination-related code examples available on the Internet are terribly inefficient, or in many cases, just plain wrong.
Combinations
The three essential operations on mathematical combinations are illustrated in Figure 2. The output tells you that with n = 4 and k = 2, there are six combinations:
{ 0, 1 } { 1, 2 } { 0, 2 } { 1, 3 } { 0, 3 } { 2, 3 }
From this example you can see that I need to be able to create a combination, calculate how many total combination elements there are for a given set of items and subset size, and determine the successor to a particular combination element so that I can list all combination elements.
Figure 2 Combinations
static void Main() { long n = 4; long k = 2; Console.WriteLine("With n = " + n + ", and k = " + k); Console.WriteLine("There are " + Combination.Choose(n,k) + "combinations\n"); Combination c = new Combination(n,k); Console.WriteLine("The mathematical combinations are:"); while (c != null) { Console.WriteLine(c.ToString()); c = c.Successor(); } Console.ReadLine(); }
Looking a little closer at the examples, you can see that combinations have two important characteristics: the total number of items in the set (usually denoted by n in mathematical literature) and the size of the subset (usually denoted by k). Mathematical combinations can be 0-based or 1-based. I will use 0-based notation throughout this column, and use n and k for the total number of items and the number of items in the subset, respectively.
In my examples thus far I have listed the elements of the combinations in what is called lexicographic order (sometimes called dictionary order). For mathematical combinations this means that the elements, if interpreted as integers, are listed in increasing order. For example, if n = 5 and k = 3, the first element is { 0, 1, 2 } and the next element is { 0, 1, 3 } because 12 comes before 13. Notice too that the atoms (individual integers) of a combination element also appear in increasing order so there is a kind of dual ordered-ness.
An important function for combinations is the total number of elements for particular n and k values. This function is most often called Choose. So for the first example with 5 names of people I can write Choose(5,3) = 10, meaning that for 5 items taken 3 at a time there are 10 total combination elements. There are other notations and names for the Choose function that you might run into, particularly in math articles but I'll use Choose.
It is very easy to confuse a combination of n and k with a Choose function of n and k. A mathematical combination of n = 7 and k = 4 (7 items taken 4 at a time) has elements like { 0, 3, 4, 6 }, whereas the associated Choose(7,4) function returns 35 and is the total number of elements of 7 items taken 4 at a time.
Combinations are frequently confused with permutations which are all the possible arrangements of a set of items where order does matter. Say you have the names Alex, Bill, Cris, and Doug. The first three permutations in lexicographic order are { Alex, Bill, Cris, Doug }, { Alex, Bill, Doug, Cris }, and { Alex, Cris, Bill, Doug }.
A Combination Class
A mathematical combination lends itself very nicely to implementation as a class. For data members you need to store the values of n (total number of items), k (number of items in each subset element), and an array to hold the "atoms" of each combination element. The basic code that represents a Combination object and a constructor to create the first lexicographic element of the Combination object along with code to represent it as a string is shown in Figure 3. I decided to use C#, but you can easily adapt it to the .NET-based language of your choice.
Figure 3 Combination Class Definition
public class Combination { private long n = 0; private long k = 0; private long[] data = null; public Combination(long n, long k) { if (n < 0 || k < 0) // normally n >= k throw new Exception("Negative parameter in constructor"); this.n = n; this.k = k; this.data = new long[k]; for (long i = 0; i < k; ++i) this.data[i] = i; } public override string ToString() { StringBuilder sb = new StringBuilder(); sb.Append("{ "); for (long i = 0; i < this.k; ++i) sb.AppendFormat("{0} ", this.data[i]); sb.Append("}"); return sb.ToString; }
After I put this code into a Class Library and compile, I can add a Project Reference to it and call it from a .NET Console Application, like I've done here:
Combination c = new Combination(5,3); Console.WriteLine("\nCombination c(5,3) is initially " + c.ToString());
The following output would display on the screen:
Combination c(5,3) is initially { 0 1 2 }
When the Combination constructor is invoked like so:
Combination c = new Combination(5,3);
I get an object in memory that represents the first mathematical combination element in lexicographic order of five items taken three at a time. The object in memory can be represented as shown in Figure 4.

Figure 4** Object in Memory **
The constructor code that creates the first combination element is quite simple. The two parameters that represent the total number of items and the size of the subset are stored in data members n and k, respectively. Because the values I'm dealing with can be very large, I decided to use the C# type long instead of type int. If I wanted to I could have doubled the range of values by using type ulong (unsigned long). I use the size of the subset, k, to allocate space for an array of long-named data, and then fill each cell of data with integers ranging from 0 through k-1.
Calculating the Number of Combination Elements
Now that I've determined how to create a Combination object, let's look at the second of three fundamental operations on combinations—calculating the total number of combination elements for a given total number of items n, and the subset size k. For example, if you are dealing with n = 5 items taken k = 3 at a time, there are 10 possible combination elements:
{ 0, 1, 2 } { 0, 3, 4 } { 0, 1, 3 } { 1, 2, 3 } { 0, 1, 4 } { 1, 2, 4 } { 0, 2, 3 } { 1, 3, 4 } { 0, 2, 4 } { 2, 3, 4 }
I want to implement a Choose(n,k) function that returns the number of elements; Choose(5,3) returns 10. Looking for existing Choose implementations, I was surprised to find that the most common algorithms on the Internet are very weak. Before I show you my implementation of Choose, let's briefly examine the standard implementation of a Choose function.
The standard way of coding the Choose(n,k) function uses its definition formula directly. This is an obvious but poor solution. Here's the typical Choose(n,k) function coded using C#:
// poor implementation of Choose(n,k) static int Choose(int n, int k) { int numerator = Factorial(n); int denominator = Factorial(k) * Factorial(n-k); return ( numerator / denominator ); }
The helper function Factorial is implemented as follows:
static int Factorial(int m) { int ans = 1; for (int i = m; i >= 1; —i) { ans = ans * i; } return ans; }
But there are several problems with this implementation of Choose(n,k). The most serious is that it will overflow for relatively small values of n and k. Notice that this Choose(n,k) first calculates Factorial(n), which can quickly grow into a huge number even for relatively small values of n (for example, 21! will overflow an unsigned 64-bit number). Then Choose(n,k) divides by the product of two factorials, which could also be a huge number, bringing the result back down to a relatively small number. The point is that even if Choose(n,k) returns a reasonably small value, the intermediate calculations can easily overflow.
A better implementation of Choose(n,k) calculates its answer in a different way. It turns out that Choose(n,k) can be calculated using the following alternative formula
Choose(n,k) = (<em xmlns="https://www.w3.org/1999/xhtml">n</em> * (n-1) * (n-2) * ... * (n-k+1)) / ( 1 * 2 * ... * k)
which looks ugly, but is more understandable with an example:
Choose(7,3) = (7 * 6 * 5) / (1 * 2 * 3)
Instead of computing the numerator (a big number), then the denominator (a big number), and then dividing, you can calculate partial products and divide as you go. For the Choose(7,3) example, you first calculate 7 * 6 and divide by 2, getting 24 (skipping the first 1 term on the bottom of the fraction because dividing by 1 has no effect). Then multiplying that partial product by 5 and dividing by 3, you get an answer of 35, as before.
There is a second optimization for the Choose(n,k) method that is a consequence of the following property:
Choose(n,k) = Choose(n, n-k).
For example, Choose(10,8) = Choose(10,2). This is not an obvious relationship, but if you experiment with a few examples you'll see why this is true. Calculating Choose(10,8) directly involves computing seven partial products and seven divisions, but calculating the equivalent Choose(10,2) requires only one multiplication and one division operation.
Putting these ideas together, I implemented Choose(n,k) as shown in Figure 5. In the Choose function, I do a quick check for n equal to k and return 1 when this is true. My Choose algorithm works without this check, but it improves the performance of a method that generates a specified Combination object element. The remainder of the Choose implementation calculates the total number of elements using the algorithm I just explained.
Figure 5 Efficient Choose Method Implementation
public static long Choose(long n, long k) { if (n < 0 || k < 0) throw new Exception("Invalid negative parameter in Choose()"); if (n < k) return 0; if (n == k) return 1; long delta, iMax; if (k < n-k) // ex: Choose(100,3) { delta = n-k; iMax = k; } else // ex: Choose(100,97) { delta = k; iMax = n-k; } long ans = delta + 1; for (long i = 2; i <= iMax; ++i) { checked { ans = (ans * (delta + i)) / i; } } return ans; }
Generating All Combination Elements
The third fundamental operation on combinations is generating a list of all combination elements for a given number of items, n, and subset size, k. Just like the problem of implementing the Choose function in the previous section, a search on the Internet turned up less than optimal solutions. Let's briefly look at a typical solution for generating all combination elements for given n and k values, and then I'll improve on it.
Suppose you have four items—the names Adam, Barb, Carl, Dave—and you want all combinations of these four items taken two at a time. A fragment of C# code that will generate the six elements of this combination is shown here:
// naive technique to generate all combinations Console.WriteLine("\nAll elements of 4 names, 2 at a time: "); string[] names = {"Adam", "Barb", "Carl", "Dave"}; for (int i = 0; i < names.Length; ++i) { for (int j = i+1; j < names.Length; ++j) { Console.WriteLine( "{ " + names[i] + ", " + names[j] + " }" ); } }
If you execute this code, the (correct) result will be:
{ Adam, Barb }, { Adam, Carl }, { Adam, Dave }, { Barb, Carl }, { Barb, Dave }, { Carl, Dave }.
But there are three problems. First, the technique works well if you want to generate all elements of a combination, but what if you only want some of the elements or a particular element? Second, this technique is very specific to a particular problem and doesn't generalize well. And third, it works nicely when the number of items in each subset element, k, is small, but what if k is very large? If you were interested in n = 100 items taken k = 50 at a time, you'd have to code 50 for loops or use recursion.
A better solution to the problem of generating all combination elements is to implement a Successor method that returns the next lexicographic element of a given element. If you combine Successor with an ApplyTo method that maps a mathematical combination onto a string array, you'll have an efficient, general way to produce all combination elements.
The code in Figure 6 shows the Successor method. Successor begins by checking to see if there is a next combination element. Suppose, for example, you are dealing with n = 5 items taken k = 3 at a time. There are 10 combination elements:
{ 0, 1, 2 } { 0, 3, 4 } { 0, 1, 3 } { 1, 2, 3 } { 0, 1, 4 } { 1, 2, 4 } { 0, 2, 3 } { 1, 3, 4 } { 0, 2, 4 } { 2, 3, 4 }
Figure 6 Lexicographic Successor of an Element
public Combination Successor() { if (this.data.Length == 0 || this.data[0] == this.n - this.k) return null; Combination ans = new Combination(this.n, this.k); long i; for (i = 0; i < this.k; ++i) ans.data[i] = this.data[i]; for (i = this.k - 1; i > 0 && ans.data[i] == this.n - this.k + i; --i) ; ++ans.data[i]; for (long j = i; j < this.k - 1; ++j) ans.data[j+1] = ans.data[j] + 1; return ans; }
Notice that you can identify the last lexicographic element, { 2, 3, 4 }, because it is the only element which has a first atom of 2—which equals the value n-k, or in other words, it has a value of n-k at position 0. This relationship is true in general for all combinations. Likewise, you can identify the first lexicographic element, { 0, 1, 2 }, because it is the only one with a last atom of 2 or, in other words, it has a value of k-1 at position k-1. Again, this is true in general. The Successor method returns null if there is no valid next element. Alternatives to returning null would be to throw an exception or return an error code.
The algorithm to generate the Successor element does not use any special tricks. Essentially you start at the right-most atom and move left until you locate the left-most atom which should be incremented. Then you increment the atom at index i and reset all atoms to the right of i to be 1 larger than the value to its left. For example, suppose n = 5 and k = 3 and you want the successor to the combination { 0, 3, 4 }. Index i starts at cell 2 (pointing to atom value 4), and moves left until it hits cell 0 (pointing at atom value 0). That atom value is incremented to 1, and all atoms to the right (the 3 and 4) are incremented from the value to the left in the array, yielding the result { 1, 2, 3 }.
Once you have your Successor method, you need an ApplyTo method that will apply a combination element to an array of strings. The ApplyTo method is simple:
public string[] ApplyTo(string[] strarr) { if (strarr.Length != this.n) throw new Exception("Bad array size"); string[] result = new string[this.k]; for (long i = 0; i < result.Length; ++i) result[i] = strarr[this.data[i]]; return result; }
After checking to make sure that the array of strings input parameter has the correct number of strings, you create a result array with the size of the subset k. You then iterate through the input strings and store a reference to each at the appropriate cell of the result array. Like many operations that are performed with combinations, it's not entirely obvious what is happening until you trace through an example or two.
After instantiating a Combination object of the appropriate size and subset size, create an array of strings to hold the result combinations. Use a while loop to iterate through all combination elements—recall that the Successor method returns null when there aren't any more next elements—and the ApplyTo method maps the current element onto the original array of strings.
Conclusion
Combinations are an indispensable tool in planning and executing configuration testing, especially in a sub-area called interaction analysis. Suppose, for example, you need to test your product on a machine with multiple browsers and multiple media players installed. You want to test your system in conjunction with three browsers installed from a pool of eight browsers, and with two media players installed from a pool of six players. How many configuration combinations are there? How can you programmatically list these configurations? The techniques presented in this column make it easy for you to calculate that there are Choose(8,3) * Choose(6,2) = 840 possible test configurations. It also allows you to easily list all of them programmatically.
Combinations are useful when examining and testing paths of execution. I'll illustrate with a classic problem that is a surrogate for analyzing paths of execution (problems like this example are often used in interviewing test engineer candidates at Microsoft). Suppose you are developing a game. Players enter the southwest corner of a room with a tiled floor. Players must move to the northeast corner of the room by moving one tile to the east or one tile to the north (in other words players are always moving in the direction of the exit and do not backtrack). If the room is small—only 10 tiles by 6 tiles—how many different paths can the player take? Can you test all of them? If a move to the east is represented using the letter E and a move to the north is represented by the letter N, one possible path to the exit where the player moves all the way to the east wall and then straight north is:
E E E E E E E E E E N N N N N N
A different path is:
E N E N E N E N E N E N E E E E
Observe that no matter how the player moves, there will always be exactly 16 moves. Also notice that you can think of a move as "E" or "not E." If you imagine a sequence of 16 blanks, you must fill in 10 of the 16 blanks with "E" (because the remaining blanks must be "N"). So, the answer to this question is that there are Choose(16,10) = 8,008 possible paths and you can easily generate them using the code in this column.
As I said earlier, testing is a vitally important aspect of software development. Join me here next time for more tips you can put to use in your testing process.
Send your questions and comments for James to testrun@microsoft.com.
Dr. James McCaffrey works for Volt Information Sciences Inc. where he manages technical training for software engineers at Microsoft. He has worked on several Microsoft products including Internet Explorer and MSN Search. James can be reached at jmccaffrey@volt.com or v-jammc@microsoft.com.