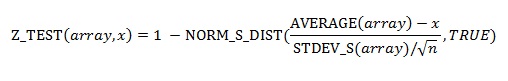WorksheetFunction.Z_Test method (Excel)
Returns the one-tailed probability-value of a z-test. For a given hypothesized population mean, Z_Test returns the probability that the sample mean would be greater than the average of observations in the data set (array); that is, the observed sample mean.
Syntax
expression.Z_Test (Arg1, Arg2, Arg3)
expression A variable that represents a WorksheetFunction object.
Parameters
| Name | Required/Optional | Data type | Description |
|---|---|---|---|
| Arg1 | Required | Variant | Array is the array or range of data against which to test the hypothesized population mean. |
| Arg2 | Required | Double | The value to test. |
| Arg3 | Optional | Variant | Sigma is the population (known) standard deviation. If omitted, the sample standard deviation is used. |
Return value
Double
Remarks
If array is empty, Z_Test returns the #N/A error value.
Z_Test is calculated as follows when sigma is not omitted:
Z_Test is calculated as follows when sigma is omitted, where x is the sample mean AVERAGE(array); s is the sample standard deviation STDEV_S(array); and n is the number of observations in the sample COUNT(array):
Z_Test represents the probability that the sample mean would be greater than the observed value AVERAGE(array), when the underlying population mean is μ0. From the symmetry of the Normal distribution, if AVERAGE(array) < μ0, Z_Test will return a value greater than 0.5.
The following Excel formula can be used to calculate the two-tailed probability that the sample mean would be further from μ0 (in either direction) than AVERAGE(array), when the underlying population mean is μ0:
=2 * MIN(Z_TEST(_array_,μ0,_sigma_), 1 - Z_TEST(_array_,μ0,_sigma_))
Support and feedback
Have questions or feedback about Office VBA or this documentation? Please see Office VBA support and feedback for guidance about the ways you can receive support and provide feedback.
Feedback
Coming soon: Throughout 2024 we will be phasing out GitHub Issues as the feedback mechanism for content and replacing it with a new feedback system. For more information see: https://aka.ms/ContentUserFeedback.
Submit and view feedback for