The Scale Transform
Discover the SkiaSharp scale transform for scaling objects to various sizes
As you've seen in The Translate Transform article, the translate transform can move a graphical object from one location to another. In contrast, the scale transform changes the size of the graphical object:
The scale transform also often causes graphics coordinates to move as they are made larger.
Earlier you saw two transform formulas that describe the effects of translation factors of dx and dy:
x' = x + dx
y' = y + dy
Scale factors of sx and sy are multiplicative rather than additive:
x' = sx · x
y' = sy · y
The default values of the translate factors are 0; the default values of the scale factors are 1.
The SKCanvas class defines four Scale methods. The first Scale method is for cases when you want the same horizontal and vertical scaling factor:
public void Scale (Single s)
This is known as isotropic scaling — scaling that is the same in both directions. Isotropic scaling preserves the object's aspect ratio.
The second Scale method lets you specify different values for horizontal and vertical scaling:
public void Scale (Single sx, Single sy)
This results in anisotropic scaling.
The third Scale method combines the two scaling factors in a single SKPoint value:
public void Scale (SKPoint size)
The fourth Scale method will be described shortly.
The Basic Scale page demonstrates the Scale method. The BasicScalePage.xaml file contains two Slider elements that let you select horizontal and vertical scaling factors between 0 and 10. The BasicScalePage.xaml.cs code-behind file uses those values to call Scale before displaying a rounded rectangle stroked with a dashed line and sized to fit some text in the upper-left corner of the canvas:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear(SKColors.SkyBlue);
using (SKPaint strokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 3,
PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
})
using (SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Fill,
Color = SKColors.Blue,
TextSize = 50
})
{
canvas.Scale((float)xScaleSlider.Value,
(float)yScaleSlider.Value);
SKRect textBounds = new SKRect();
textPaint.MeasureText(Title, ref textBounds);
float margin = 10;
SKRect borderRect = SKRect.Create(new SKPoint(margin, margin), textBounds.Size);
canvas.DrawRoundRect(borderRect, 20, 20, strokePaint);
canvas.DrawText(Title, margin, -textBounds.Top + margin, textPaint);
}
}
You might wonder: How do the scaling factors affect the value returned from the MeasureText method of SKPaint? The answer is: Not at all. Scale is a method of SKCanvas. It does not affect anything you do with an SKPaint object until you use that object to render something on the canvas.
As you can see, everything drawn after the Scale call increases proportionally:
The text, the width of the dashed line, the length of the dashes in that line, the rounding of the corners, and the 10-pixel margin between the left and top edges of the canvas and the rounded rectangle are all subject to the same scaling factors.
Important
The Universal Windows Platform does not properly render anisotropicly scaled text.
Anisotropic scaling causes the stroke width to become different for lines aligned with the horizontal and vertical axes. (This is also evident from the first image on this page.) If you don't want the stroke width to be affected by the scaling factors, set it to 0 and it will always be one pixel wide regardless of the Scale setting.
Scaling is relative to the upper-left corner of the canvas. This might be exactly what you want, but it might not be. Suppose you want to position the text and rectangle somewhere else on the canvas and you want to scale it relative to its center. In that case you can use the fourth version of the Scale method, which includes two additional parameters to specify the center of scaling:
public void Scale (Single sx, Single sy, Single px, Single py)
The px and py parameters define a point that is sometimes called the scaling center but in the SkiaSharp documentation is referred to as a pivot point. This is a point relative to the upper-left corner of the canvas that is not affected by the scaling. All scaling occurs relative to that center.
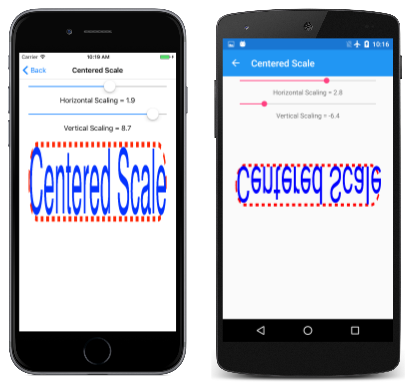
The Centered Scale page shows how this works. The PaintSurface handler is similar to the Basic Scale program except that the margin value is calculated to center the text horizontally, which implies that the program works best in portrait mode:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear(SKColors.SkyBlue);
using (SKPaint strokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 3,
PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
})
using (SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Fill,
Color = SKColors.Blue,
TextSize = 50
})
{
SKRect textBounds = new SKRect();
textPaint.MeasureText(Title, ref textBounds);
float margin = (info.Width - textBounds.Width) / 2;
float sx = (float)xScaleSlider.Value;
float sy = (float)yScaleSlider.Value;
float px = margin + textBounds.Width / 2;
float py = margin + textBounds.Height / 2;
canvas.Scale(sx, sy, px, py);
SKRect borderRect = SKRect.Create(new SKPoint(margin, margin), textBounds.Size);
canvas.DrawRoundRect(borderRect, 20, 20, strokePaint);
canvas.DrawText(Title, margin, -textBounds.Top + margin, textPaint);
}
}
The upper-left corner of the rounded rectangle is positioned margin pixels from the left of the canvas and margin pixels from the top. The last two arguments to the Scale method are set to those values plus the width and height of the text, which is also the width and height of the rounded rectangle. This means that all scaling is relative to the center of that rectangle:
The Slider elements in this program have a range of –10 to 10. As you can see,
negative values of vertical scaling (such as on the Android screen in the center) cause objects to flip around the horizontal axis that passes through the center of scaling. Negative values of horizontal scaling (such as in the UWP screen on the right) cause objects to flip around the vertical axis that passes through the center of scaling.
The version of the Scale method with pivot points is a shortcut for a series of three Translate and Scale calls. You might want to see how this works by replacing the Scale method in the Centered Scale page with the following:
canvas.Translate(-px, -py);
These are the negatives of the pivot point coordinates.
Now run the program again. You'll see that the rectangle and text are shifted so that the center is in the upper-left corner of the canvas. You can barely see it. The sliders don't work of course because now the program doesn't scale at all.
Now add the basic Scale call (without a scaling center) before that Translate call:
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
If you're familiar with this exercise in other graphics programming systems, you might think that's wrong, but it's not. Skia handles successive transform calls a little differently from what you might be familiar with.
With the successive Scale and Translate calls, the center of the rounded rectangle is still in the upper-left corner, but you can now scale it relative to the upper-left corner of the canvas, which is also the center of the rounded rectangle.
Now, before that Scale call, add another Translate call with the centering values:
canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
This moves the scaled result back to the original position. Those three calls are equivalent to:
canvas.Scale(sx, sy, px, py);
The individual transforms are compounded so that the total transform formula is:
x' = sx · (x – px) + px
y' = sy · (y – py) + py
Keep in mind that the default values of sx and sy are 1. It's easy to convince yourself that the pivot point (px, py) is not transformed by these formulas. It remains in the same location relative to the canvas.
When you combine Translate and Scale calls, the order matters. If the Translate comes after the Scale, the translation factors are effectively scaled by the scaling factors. If the Translate comes before the Scale, the translation factors are not scaled. This process becomes somewhat clearer (albeit more mathematical) when the subject of transform matrices is introduced.
The SKPath class defines a read-only Bounds property that returns an SKRect defining the extent of the coordinates in the path. For example, when the Bounds property is obtained from the hendecagram path created earlier, the Left and Top properties of the rectangle are approximately –100, the Right and Bottom properties are approximately 100, and the Width and Height properties are approximately 200. (Most of the actual values are a little less because the points of the stars are defined by a circle with a radius of 100 but only the top point is parallel with the horizontal or vertical axes.)
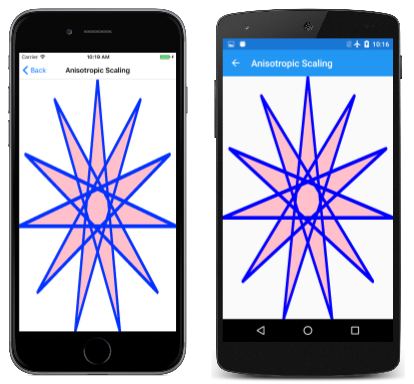
The availability of this information implies that it should be possible to derive scale and translate factors suitable for scaling a path to the size of the canvas. The Anisotropic Scaling page demonstrates this with the 11-pointed star. An anisotropic scale means that it's unequal in the horizontal and vertical directions, which means that the star won't retain its original aspect ratio. Here's the relevant code in the PaintSurface handler:
SKPath path = HendecagramPage.HendecagramPath;
SKRect pathBounds = path.Bounds;
using (SKPaint fillPaint = new SKPaint
{
Style = SKPaintStyle.Fill,
Color = SKColors.Pink
})
using (SKPaint strokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Blue,
StrokeWidth = 3,
StrokeJoin = SKStrokeJoin.Round
})
{
canvas.Scale(info.Width / pathBounds.Width,
info.Height / pathBounds.Height);
canvas.Translate(-pathBounds.Left, -pathBounds.Top);
canvas.DrawPath(path, fillPaint);
canvas.DrawPath(path, strokePaint);
}
The pathBounds rectangle is obtained near the top of this code, and then used later with the width and height of the canvas in the Scale call. That call by itself will scale the coordinates of the path when it's rendered by the DrawPath call but the star will be centered in the upper-right corner of the canvas. It needs to be shifted down and to the left. This is the job of the Translate call. Those two properties of pathBounds are approximately –100, so the translation factors are about 100. Because the Translate call is after the Scale call, those values are effectively scaled by the scaling factors, so they move the center of the star to the center of the canvas:
Another way you can think about the Scale and Translate calls is to determine the effect in reverse sequence: The Translate call shifts the path so it becomes fully visible but oriented in the upper-left corner of the canvas. The Scale method then makes that star larger relative to the upper-left corner.
Actually, it appears that the star is a little larger than the canvas. The problem is the stroke width. The Bounds property of SKPath indicates the dimensions of the coordinates encoded in the path, and that's what the program uses to scale it. When the path is rendered with a particular stroke width, the rendered path is larger than the canvas.
To fix this problem you need to compensate for that. One easy approach in this program is to add the following statement right before the Scale call:
pathBounds.Inflate(strokePaint.StrokeWidth / 2,
strokePaint.StrokeWidth / 2);
This increases the pathBounds rectangle by 1.5 units on all four sides. This is a reasonable solution only when the stroke join is rounded. A miter join can be longer and is difficult to calculate.
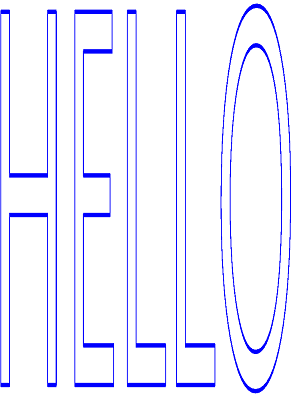
You can also use a similar technique with text, as the Anisotropic Text page demonstrates. Here's the relevant part of the PaintSurface handler from the AnisotropicTextPage class:
using (SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Blue,
StrokeWidth = 0.1f,
StrokeJoin = SKStrokeJoin.Round
})
{
SKRect textBounds = new SKRect();
textPaint.MeasureText("HELLO", ref textBounds);
// Inflate bounds by the stroke width
textBounds.Inflate(textPaint.StrokeWidth / 2,
textPaint.StrokeWidth / 2);
canvas.Scale(info.Width / textBounds.Width,
info.Height / textBounds.Height);
canvas.Translate(-textBounds.Left, -textBounds.Top);
canvas.DrawText("HELLO", 0, 0, textPaint);
}
It's similar logic, and the text expands to the size of the page based on the text bounds rectangle returned from MeasureText (which is a little larger than the actual text):
If you need to preserve the aspect ratio of the graphical objects, you'll want to use isotropic scaling. The Isotropic Scaling page demonstrates this for the 11-pointed star. Conceptually, the steps for displaying a graphical object in the center of the page with isotropic scaling are:
- Translate the center of the graphical object to the upper-left corner.
- Scale the object based on the minimum of the horizontal and vertical page dimensions divided by the graphical object dimensions.
- Translate the center of the scaled object to the center of the page.
The IsotropicScalingPage performs these steps in reverse order before displaying the star:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKPath path = HendecagramArrayPage.HendecagramPath;
SKRect pathBounds = path.Bounds;
using (SKPaint fillPaint = new SKPaint())
{
fillPaint.Style = SKPaintStyle.Fill;
float scale = Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height);
for (int i = 0; i <= 10; i++)
{
fillPaint.Color = new SKColor((byte)(255 * (10 - i) / 10),
0,
(byte)(255 * i / 10));
canvas.Save();
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(scale);
canvas.Translate(-pathBounds.MidX, -pathBounds.MidY);
canvas.DrawPath(path, fillPaint);
canvas.Restore();
scale *= 0.9f;
}
}
}
The code also displays the star 10 more times, each time decreasing the scaling factor by 10% and progressively changing the color from red to blue: