변환(Direct3D 9)

  • 아티클

Direct3D 파트는 고정 함수 기하 도형 파이프라인을 통해 기하 도형을 푸시하는 변환 엔진입니다. 세계 좌표의 모델 및 뷰어를 찾아내고, 표시할 꼭짓점을 화면에 투사하고, 뷰포트에 대한 꼭짓점을 잘라냅니다. 또한 변환 엔진은 조명 계산을 수행하여 각 꼭짓점의 확산 및 반사 구성 요소를 결정합니다.

기하 도형 파이프라인에서는 꼭짓점을 입력으로 사용합니다. 변환 엔진은 월드, 보기 및 프로젝션 변환을 꼭짓점에 적용하고, 결과를 잘라내고, 모든 항목을 래스터라이저로 전달합니다.

파이프라인의 맨 위에서 모델의 꼭짓점은 로컬 좌표계를 기준으로 선언됩니다. 이는 로컬 원점 및 방향입니다. 이 좌표 방향을 모델 공간이라고도 하며 개별 좌표를 모델 좌표라고 합니다.

기하 도형 파이프라인의 첫 번째 단계에서는 모델의 꼭짓점을 해당 로컬 좌표계에서 장면의 모든 개체가 사용하는 좌표계로 변환합니다. 꼭짓점을 다시 정렬하는 프로세스를 월드 변환이라고 합니다. 이 새 방향을 일반적으로 월드 공간이라고 하며, 월드 공간의 각 꼭짓점은 월드 좌표를 사용하여 선언됩니다.

다음 단계에서 3D 월드를 설명하는 꼭짓점의 원점은 카메라를 기준으로 설정됩니다. 즉, 애플리케이션은 장면에 대한 시점을 선택하고, 월드 공간 좌표는 카메라 뷰를 중심으로 재배치 및 회전되어 월드 공간을 카메라 공간으로 전환합니다. 보기 변환입니다.

다음 단계는 프로젝션 변환입니다. 파이프라인의 이 부분에서 개체는 일반적으로 장면에 깊이의 환상을 주기 위해 뷰어와의 거리와 관련하여 크기가 조정됩니다. close 개체는 먼 개체보다 크게 표시되도록 만들어집니다. 편의를 위해 이 문서에서는 프로젝션 변환 이후에 꼭짓점이 존재하는 공간을 프로젝션 공간이라고 부르겠습니다. 일부 그래픽 서적에서는 프로젝션 공간을 관점후 동종 공간이라고 부르기도 합니다. 모든 프로젝션 변환에서 장면의 개체 크기가 조정되는 것은 아닙니다. 이와 같은 프로젝션을 아핀 또는 직교 프로젝션이라고 합니다.

파이프라인의 마지막 부분에서는 장면에 보이지 않는 꼭짓점이 제거됩니다. 따라서 래스터라이저는 표시되지 않는 항목의 색 및 음영을 계산하는 데 시간을 사용하지 않습니다. 이 프로세스를 클리핑이라고 합니다. 클리핑 후에 나머지 꼭짓점은 뷰포트 매개 변수에 따라 크기가 조정되며 화면 좌표로 변환됩니다. 장면이 래스터화되면 장면에 표시된 결과인 꼭짓점은 장면 공간에 존재하게 됩니다.

변환은 개체 기하 도형을 하나의 좌표에서 다른 좌표로 변환하는 데 사용됩니다. Direct3D는 매트릭스를 사용하여 3D 변환을 수행합니다. 이 섹션에서는 행렬이 3D 변환을 만드는 방법을 설명하고, 변환에 대한 몇 가지 일반적인 용도를 설명하고, 행렬을 결합하여 여러 변환을 포함하는 단일 행렬을 생성하는 방법을 자세히 설명합니다.

매트릭스 변환

3D 그래픽을 사용하는 애플리케이션에서 기하 도형 변환을 사용하여 다음 작업을 수행할 수 있습니다.

  • 다른 개체를 기준으로 개체의 위치를 표현합니다.
  • 개체를 회전하고 크기를 조정합니다.
  • 보는 위치, 방향 및 관점을 변경합니다.

다음 수식과 같이 4x4 매트릭스를 사용하여 한 지점(x, y, z)을 다른 지점(x', y', z')으로 변환할 수 있습니다.

임의의 점을 다른 지점으로 변환하는 수식

(x, y, z)에 대한 다음 수식과 매트릭스를 수행하여 지점(x', y', z')을 생성합니다.

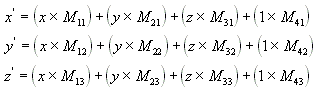
새 지점에 대한 수식

가장 일반적인 변환은 좌표 이동, 회전 및 크기 조정입니다. 이러한 효과를 생성하는 매트릭스를 단일 매트릭스로 결합하여 한 번에 여러 변환을 계산할 수 있습니다. 예를 들어 일련의 지점을 좌표 이동하고 회전하는 단일 매트릭스를 만들 수 있습니다.

매트릭스는 행-열 순서로 기록됩니다. 각 축을 따라 꼭짓점의 크기를 동일하게 조정(균등 크기 조정)하는 매트릭스는 수학 표기법을 사용하는 다음 매트릭스로 표시됩니다.

균일한 크기 조정을 위한 행렬의 수식

C++에서 Direct3D는 D3DMATRIX 구조를 사용하여 행렬을 2차원 배열로 선언합니다. 다음 예제에서는 D3DMATRIX 구조체를 초기화하여 균일한 크기 조정 매트릭스 역할을 하는 방법을 보여줍니다.

// In this example, s is a variable of type float.

D3DMATRIX scale = {
    s,               0.0f,            0.0f,            0.0f,
    0.0f,            s,               0.0f,            0.0f,
    0.0f,            0.0f,            s,               0.0f,
    0.0f,            0.0f,            0.0f,            1.0f
};

번역

다음 수식은 지점(x, y, z)을 새 지점(x', y', z')으로 변환합니다.

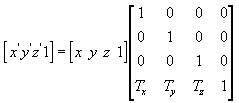
새 지점에 대한 변환 행렬의 수식

C++에서 좌표 이동 매트릭스를 수동으로 만들 수 있습니다. 다음 예제는 꼭짓점의 좌표를 이동하는 매트릭스를 만드는 함수의 소스 코드입니다.

D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
    D3DXMATRIX ret;

    D3DXMatrixIdentity(&ret);
    ret(3, 0) = dx;
    ret(3, 1) = dy;
    ret(3, 2) = dz;
    return ret;
}    // End of Translate

편의를 위해 D3DX 유틸리티 라이브러리는 D3DXMatrixTranslation 함수를 제공합니다.

확장

다음은 x, y 및 z축 방향으로 임의의 값을 사용하여 지점(x, y, z)을 새 지점(x', y', z')으로 크기 조정하는 수식입니다.

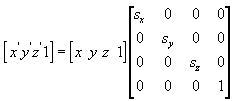
새 점의 배율 행렬 수식

회전

여기서 설명하는 변환은 왼손 좌표계를 기준으로 하기 때문에 다른 곳에서 살펴본 변환 매트릭스와 다를 수 있습니다.

다음 수식은 x축을 기준으로 지점(x, y, z)을 회전하여 새로운 지점(x', y', z')을 생성합니다.

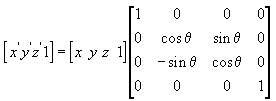
새 지점에 대한 x 회전 행렬의 수식

다음 수식은 y축을 기준으로 지점을 회전합니다.

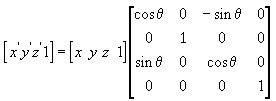
새 지점에 대한 y 회전 행렬의 수식

다음 수식은 z축을 기준으로 지점을 회전합니다.

새 지점에 대한 z 회전 행렬의 수식

이러한 예제 매트릭스에서 그리스 문자 세타는 회전 각도(라디안 단위)를 의미합니다. 원점을 향해 회전 축을 바라보는 경우 각도는 시계 방향으로 측정됩니다.

C++ 애플리케이션에서 D3DXMatrixRotationX, D3DXMatrixRotationY 및 D3DX 유틸리티 라이브러리에서 제공하는 D3DXMatrixRotationZ 함수를 사용하여 회전 행렬을 만듭니다. 다음은 D3DXMatrixRotationX 함수에 대한 코드입니다.

D3DXMATRIX* WINAPI D3DXMatrixRotationX
    ( D3DXMATRIX *pOut, float angle )
{
#if DBG
    if(!pOut)
        return NULL;
#endif

    float sin, cos;
    sincosf(angle, &sin, &cos);  // Determine sin and cos of angle

    pOut->_11 = 1.0f; pOut->_12 =  0.0f;   pOut->_13 = 0.0f; pOut->_14 = 0.0f;
    pOut->_21 = 0.0f; pOut->_22 =  cos;    pOut->_23 = sin;  pOut->_24 = 0.0f;
    pOut->_31 = 0.0f; pOut->_32 = -sin;    pOut->_33 = cos;  pOut->_34 = 0.0f;
    pOut->_41 = 0.0f; pOut->_42 =  0.0f;   pOut->_43 = 0.0f; pOut->_44 = 1.0f;

    return pOut;
}

매트릭스 연결

매트릭스를 사용할 때 얻을 수 있는 장점 중 하나는 두 개 이상의 매트릭스를 곱하여 여러 효과를 결합할 수 있다는 점입니다. 즉, 모델을 회전하고 다른 위치로 좌표 이동하기 위해 두 개의 매트릭스를 적용할 필요가 없습니다. 대신 회전 매트릭스와 좌표 이동 매트릭스를 곱하여 해당 효과를 모두 포함하는 합성 매트릭스를 만들면 됩니다. 매트릭스 연결이라고 하는 이 과정은 다음 수식을 사용하여 작성할 수 있습니다.

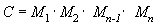
행렬 연결 수식

이 수식에서 C는 새로 생성되는 합성 매트릭스이고, M₁~Mₙ은 개별 매트릭스입니다. 대부분은 매트릭스를 두 개 또는 세 개 정도 연결하지만, 제한이 있는 것은 아닙니다.

D3DXMatrixMultiply 함수를 사용하여 행렬 곱셈을 수행합니다.

매트릭스 곱하기를 수행하는 순서가 매우 중요합니다. 위의 수식은 매트릭스 연결의 왼쪽에서 오른쪽 규칙을 반영하고 있습니다. 즉, 합성 매트릭스를 만드는 데 사용하는 매트릭스의 시각 효과는 왼쪽에서 오른쪽 순서로 발생합니다. 다음은 일반적인 월드 매트릭스를 보여주는 예제입니다. 일반적인 비행접시에 대한 월드 매트릭스를 만든다고 가정해 보겠습니다. 아마도 여러분은 비행접시의 중심인 모델 공간의 y축을 기준으로 비행접시를 회전하고, 장면의 다른 위치로 비행접시를 좌표 이동하려 할 것입니다. 이 효과를 만들려면 다음 수식과 같이 회전 매트릭스를 만든 다음, 좌표 이동 매트릭스를 곱해야 합니다.

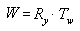
회전 행렬 및 변환 행렬을 기반으로 하는 스핀 수식

이 수식에서 Ry는 y축 기준 회전에 대한 매트릭스이고 Tw는 월드 좌표의 어떤 위치에 대한 좌표 이동입니다.

두 개의 스칼라 값을 곱할 때와는 달리, 매트릭스 곱하기는 가환성이 없기 때문에 매트릭스를 곱하는 순서가 중요합니다. 매트릭스를 반대 순서로 곱하면 비행접시를 해당 월드 공간 위치로 좌표 이동한 다음, 월드 원점을 기준으로 회전하는 시각 효과가 발생합니다.

어떤 유형의 매트릭스를 만들든, 기대하는 효과를 얻을 수 있도록 왼쪽에서 오른쪽 규칙을 기억하시기 바랍니다.

시작