你当前正在访问 Microsoft Azure Global Edition 技术文档网站。 如果需要访问由世纪互联运营的 Microsoft Azure 中国技术文档网站，请访问 https://docs.azure.cn。

Grover 搜索算法理论

  • 项目

本文从理论角度详细说明了支持 Grover 算法运作的数学原理。

有关用于解决数学问题的 Grover 算法的实际实现，请参阅 实现 Grover 的搜索算法。

问题陈述

任何搜索任务都可以使用抽象函数 $f(x)$ 表示，该函数接受搜索项 $x$。 如果项 $x$ 是搜索任务的解，则 $f(x)=1$。 如果项 $x$ 不是解，则 $f(x)=0$。 搜索问题包括查找使 $f(x_0)=1$ 的任何项 $x_0$。

Grover 算法旨在解决的任务可以表示如下：给定经典函数 $f(x):\{0,1\}^n \rightarrow\{0,1\}$，其中 $n$ 是搜索空间的比特大小，找到使 $f(x_0)=1$ 的输入 $x_0$。 此算法的复杂度是通过函数 $f(x)$ 的使用次数衡量的。 传统上，在最糟糕的情况下，需要总共计算 $f(x)$$N-1$ 次，其中 $N=2^n$，以尝试所有可能性。 $N-1$ 个元素之后，它肯定是最后一个元素。 Grover 量子算法能够更快速地解决此问题，实现了二次加速。 此处的“二次”表示，只需大约 $\sqrt{N}$ 次计算，而不是 $N$ 次。

算法概述

假设搜索任务有 $N=2^n$ 个符合条件的项，并且为每个项目分配一个从 $0$ 到 $N-1$ 的整数来为它们编制索引。 此外，假设有 $M$ 个不同的有效输入，也就是说，有 $M$ 个输入的 $f(x)=1$。 这样一来，算法的步骤如下所示：

  1. 从以状态 $\ket{0}$ 初始化的 $n$ 个量子比特的寄存器开始。
  2. 通过向寄存器中的每个量子比特应用 $H$，准备将寄存器均匀叠加：$$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
  3. 向寄存器应用以下运算 $N_{\text{optimal}}$ 次：
    1. 为求解项应用条件相移为 $-1$ 的相位黑盒 $O_f$。
    2. 向寄存器中的每个量子比特应用 $H$。
    3. 应用于除 $\ket{0}$ 之外的每个计算基础状态的条件相移 $-1$。 这可以由单一运算 $-O_0$ 表示，因为 $O_0$ 只表示对 $\ket{0}$ 的条件相移。
    4. 向寄存器中的每个量子比特应用 $H$。
  4. 度量寄存器以获取具有很高概率为解的项的索引。
  5. 检查它是否为有效的解。 如果不是，则再次开始运算。

$N_\text{optimal}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{{2}\right\rfloor$ 是最佳的迭代次数，它将最大程度地增加通过测量寄存器获得正确项的概率。

注意

步骤 3.b、3.c 和 3.d 的联合应用在文献中通常称为 Grover 扩散运算符。

向寄存器应用的整个单一运算为：

$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$

逐步跟踪寄存器的状态

为说明此过程，我们将跟踪一个简单情况下的寄存器状态的数学转换，其中只有两个量子比特，并且有效元素为 $\ket{01}。$

  1. 寄存器的启动状态为：$$|\text{register}\rangle=|00\rangle$$

  2. 向每个量子比特应用 $H$ 后，寄存器的状态转变为 $$|\text{register}\rangle=\frac{{1}{\sqrt{{4}}\sum_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$

  3. 然后，应用相位黑盒以获取：$$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$

  4. 然后 $H$ 再次作用于每个量子比特，得到 $$|\text{register}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$

  5. 现在对除 $\ket{00}$ 以外的每个状态应用条件相移：$$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$

  6. 最后再次应用 $H$，结束第一次 Grover 迭代，得到：$$|\text{register}\rangle=\ket{{01}$$

    执行上述步骤，可以在单个迭代中找到有效项。 稍后将看到，这是因为对于 N=4 和单个有效项， $N_\text{最佳}=1$。

几何学解释

为说明 Grover 算法为何有效，我们将从几何角度研究此算法。 让 $\ket{\text{bad}}$ 作为非搜索问题的解的所有状态的叠加。 假设有 $M$ 个有效的解：

$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

将状态 $\ket{\text{good}}$ 定义为是搜索问题的解的所有状态的叠加：

$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

由于 good 和 bad 是互斥集（因为一个项不能既有效又无效），因此状态 $\ket{\text{good}}$ 和 $\ket{\text{bad}}$ 是正交的 。 两种状态构成了向量空间中平面的正交基。 人们可以通过此平面将此算法可视化。

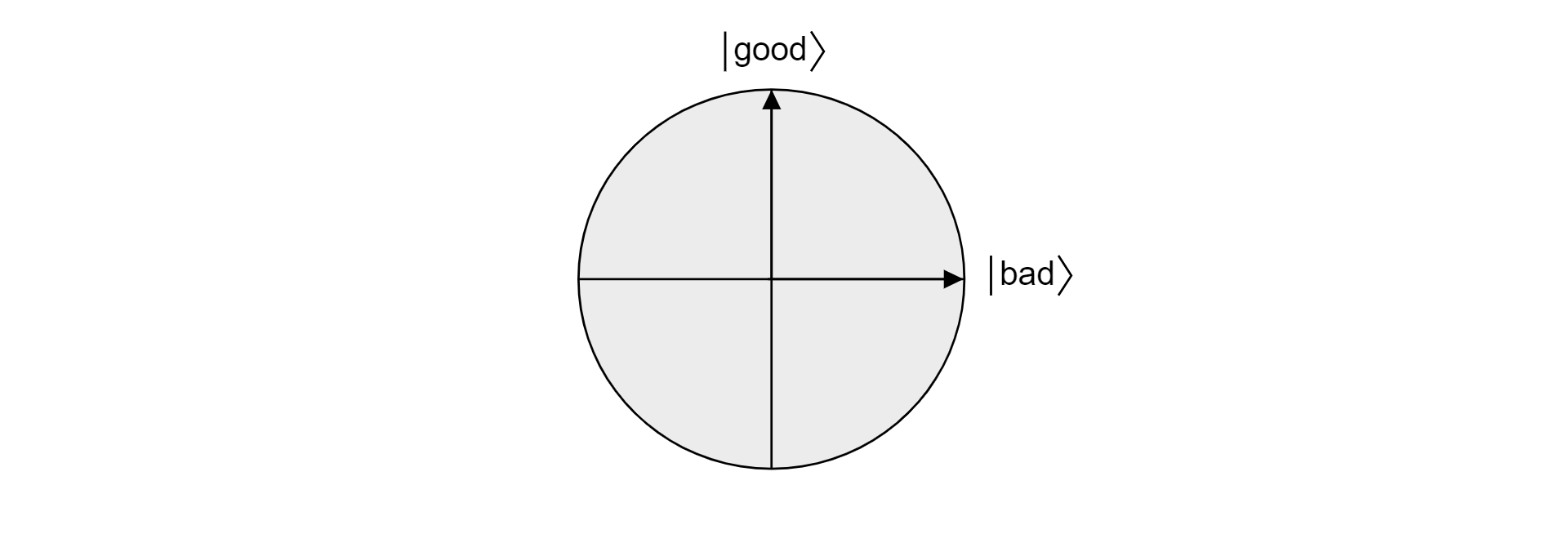
Bloch 球体中由正交好向量和坏向量投影的平面图。

现在，假设 $\ket{\psi}$ 是跨越 $\ket{\text{good}}$ 和 $\ket{\text{bad}}$ 的平面中的一个任意的状态。 该平面中的任何状态都可表示为：

$$\ket{\psi}=\alpha\ket{\text{good}} + \beta\ket{\text{bad}}$$

其中 $\alpha$ 和 $\beta$ 是实数。 接下来，我们介绍反射运算符 $R_{\ket{\psi}}$，其中 $\ket{\psi}$ 是此平面中的任意量子比特状态。 此运算符定义为：

$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$

它被称为关于 $\ket{\psi}$ 的反射运算符，因为在几何上可以将它解释为关于 $\ket{\psi}$ 的方向的反射。 请获取 $\ket{\psi}$ 和其正交互补 $\ket{\psi{}}$ 所形成的平面的正交基，以便于理解这一点。 此平面的任何状态 $\ket{\xi}$ 都可以基于此进行分解：

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

如果将运算符 $R_{\ket{\psi}}$ 应用到 $\ket{\xi}$：

$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$

运算符 $R_\ket{\psi}$ 将与 $\ket{\psi}$ 正交的分量反转，但保留 $\ket{\psi}$ 分量不变。 因此，$R_\ket{\psi}$ 是关于 $\ket{\psi}$ 的反射。

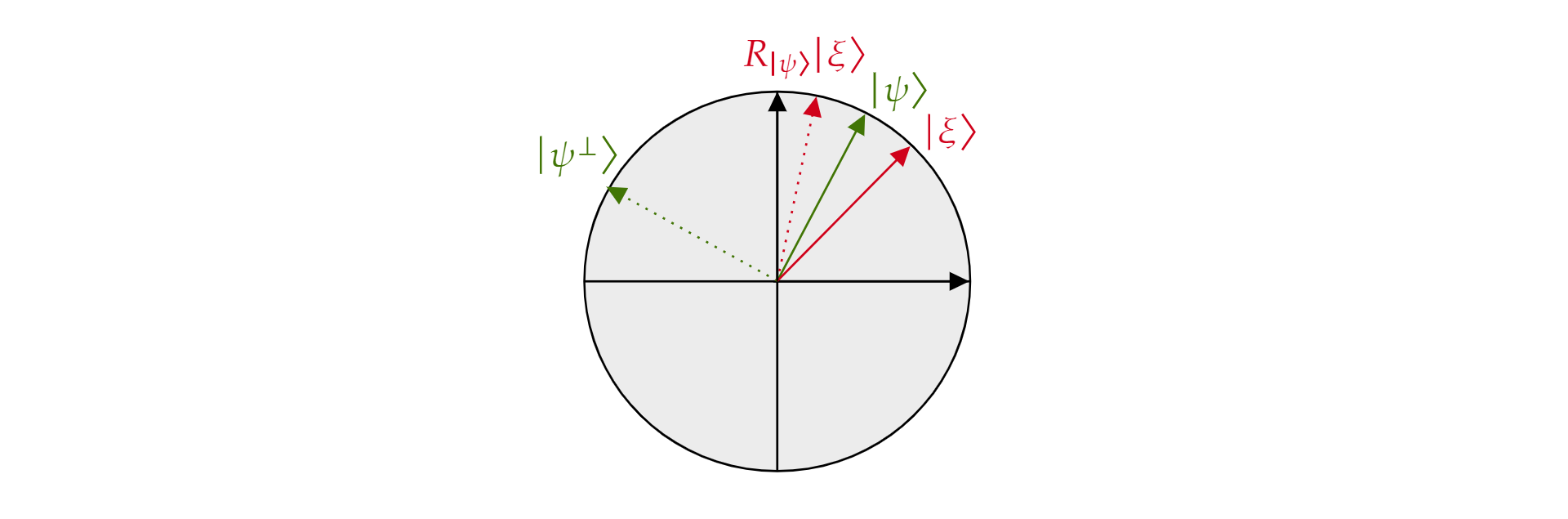
有关平面中可视化的量子状态的反射运算符图。

在 Grover 算法中，第一次向每个量子比特应用 $H$ 后，会开始将所有状态均匀叠加。 这可表示为：

$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$

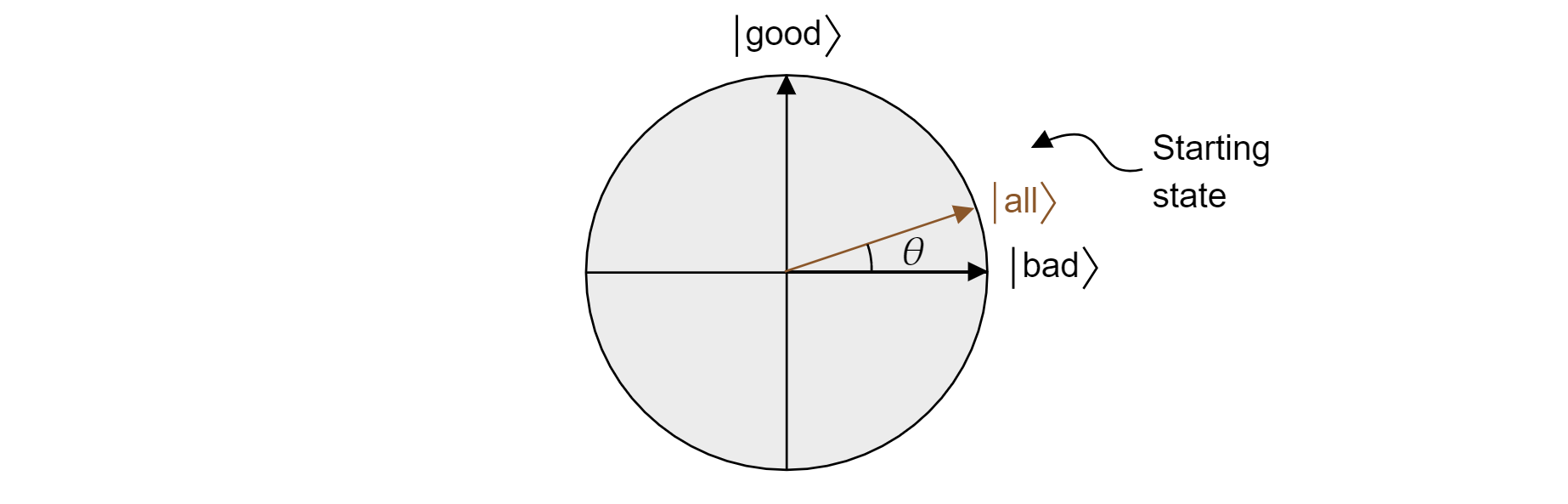
作为平面中好状态和坏状态叠加的起始状态的图。

因此此状态在平面中存在。 请注意，当从相等叠加进行测量时获得正确结果的概率只是 $|\braket{\text{很好的}|{\text{all}}}|^2=M/N$，这是随机猜测所期望的。

黑盒 $O_f$ 向搜索问题的任意解添加一个负相。 因此，它可以表示为关于 $\ket{\text{bad}}$ 轴的反射：

$$O_f = R_{\ket{\text{bad}}}= 2\ket{\text{bad}}\bra{\text{bad}} - \mathcal{I}$$

同样，条件相移 $O_0$ 就是状态 $\ket{0}$ 的反转反射：

$$O_0 = R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I}$$

了解这个事实后，很容易查明，Grover 扩散运算 $-H^{\otimes n} O_0 H^{\otimes n}$ 也是状态 $\ket{all}$ 的反射。 只需执行：

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{all}} - \mathcal{I}= R_{\ket{\text{all}}}$$

刚刚证明了 Grover 算法的每一次迭代都由 $R_\ket{\text{bad}}$ 和 $R_\ket{\text{all}}$ 这两个反射组成。

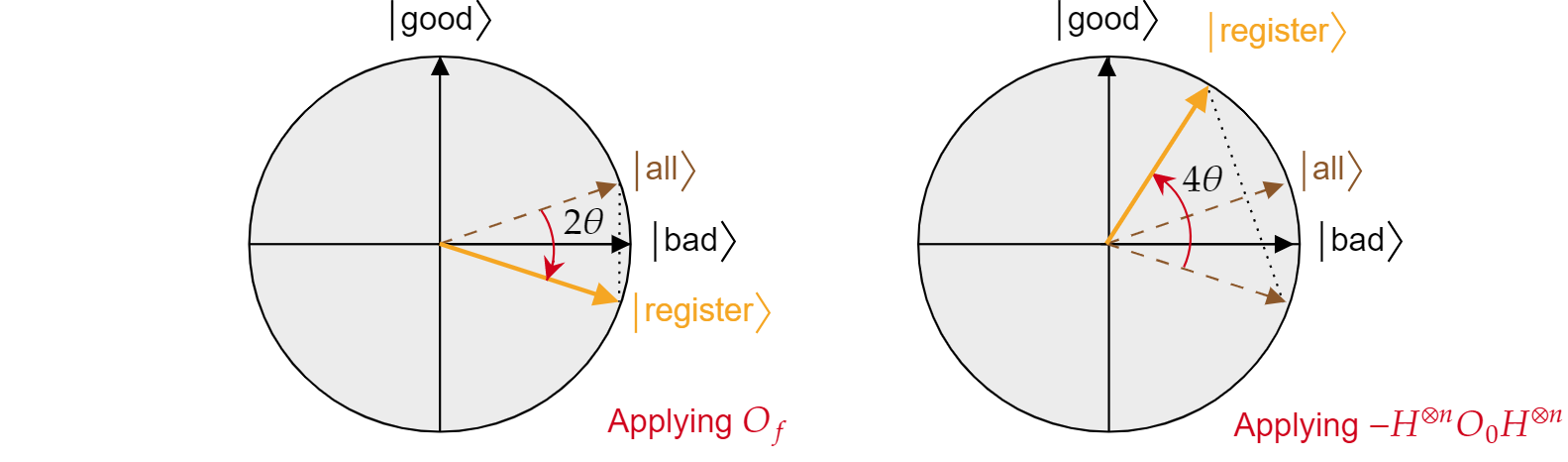
可视化为平面中两个反射序列的 Grover 迭代图。

每个 Grover 迭代产生的综合效应是逆时针旋转的角度 $2\theta$。 幸运的是，这个角度 $\theta$ 很容易找到。 由于 $\theta$ 只是 $\ket{\text{all}}$ 和 $\ket{\text{bad}}$ 之间的角度，可以使用标量积找到角度。 已知 $\cos{\theta}=\braket{\text{all}|\text{bad}}$，因此需要计算 $\braket{\text{all}|\text{bad}}$。 通过 $\ket{\text{all}}$ 对 $\ket{\text{bad}}$ 和 $\ket{\text{good}}$ 的分解，推断出：

$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$

寄存器状态和 $\ket{\text{良好}}$ 状态之间的角度随每次迭代而减小，从而增加测量有效结果的概率。 若要计算此概率，只需计算 $|\braket{\text{良好的}|\text{寄存器}}|^2$。 表示 $\ket{\text{good}}$ 和 $\ket{\text{register}}$$\gamma (k)$ 之间的角度，其中 $$ 是迭代计数：

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

因此，成功的概率是：

$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

最佳迭代次数

由于成功概率可以表示为迭代次数的函数，因此，可通过计算使成功概率函数（接近）最大化的最小正整数，找到最佳的迭代次数 $N_{\text{optimal}}$。

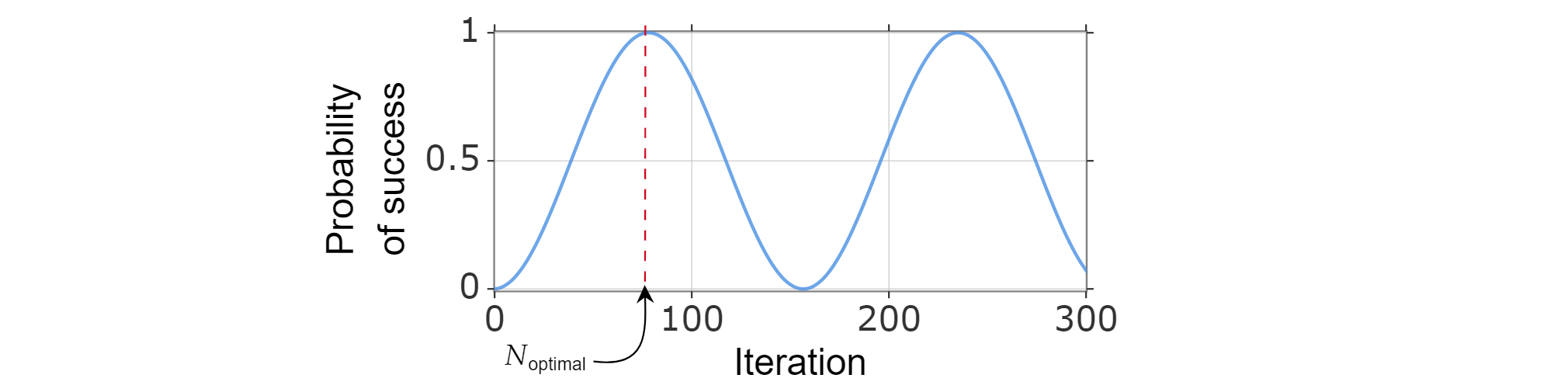
作为 Grover 迭代函数的成功概率正弦图。最佳迭代次数接近第一个峰值。

已知 $x=\frac{\pi}{2}$ 时，$\sin^2{x}$ 达到其第一个最大值，因此：

$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

会得到：

$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$

在最后一步中，$\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$。

因此，可以选择$N_\text{最佳\text{}$$N_optimal=\left}\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-{1}{2}\frac{\right\rfloor。$

复杂度分析

通过前面的分析，需要查询黑盒 $O_f$$O\left(\sqrt{\frac{N}{M}}\right)$ 次才能找到有效的项。 不过，就时间复杂度而言，此算法能否有效实现？ $O_0$ 基于计算对 $n$ 比特的布尔运算，已知可使用 $O(n)$ 个门实现。 还有两层 $n$ 阿达马门。 因此这两个部分每次迭代只需要 $O(n)$ 个门。 由于 $N=2^n$，可推断出 $O(n)=O(log(N))$。 这样的话，如果需要 $O\left(\sqrt{\frac{N}{M}}\right)$ 次迭代，并且每次迭代需要 $O(log(N))$ 个门，总时间复杂度（不考虑黑盒实现）为 $O\left(\sqrt{\frac{N}{M}}log(N)\right)$。

算法的总体复杂性最终取决于 oracle $O_f$ 实现的复杂性。 如果函数计算在量子计算机上比在经典计算机上复杂得多，那么在量子情况下，整体算法运行时将更长，即使从技术上讲，它使用的查询更少。

参考

若要继续了解 Grover 算法，可以访问以下资源：

后续步骤