转换的矩阵表示形式
m×n 矩阵是一组排列成 m 行 n 列的数字。 下图显示了多个矩阵。
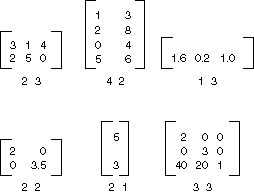
可以通过添加单个元素来添加两个相同大小的矩阵。 下图显示了两个矩阵加法示例。
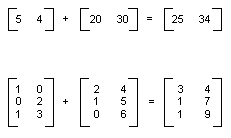
一个 m×n 矩阵可以与一个 n×p 矩阵相乘,得到一个 m×p 矩阵。 第一个矩阵的列数必须与第二个矩阵的行数相同。 例如,一个 4×2 矩阵可以乘以一个 2×3 矩阵来生成一个 4×3 矩阵。
可以将平面中的点以及矩阵的行和列视为向量。 例如,(2, 5) 是具有两个分量的向量,(3, 7, 1) 是具有三个分量的向量。 两个向量的点积定义如下:
(a, b) • (c, d) = ac + bd
(a, b, c) • (d, e, f) = ad + be + cf
例如,(2, 3) 和 (5, 4) 的点积是 (2)(5) + (3)(4) = 22。 (2, 5, 1) 和 (4, 3, 1) 的点积是 (2)(4) + (5)(3) + (1)(1) = 24。 请注意,两个向量的点积是一个数字,而不是另一个向量。 另请注意,只有当两个向量具有相同数量的分量时,才能计算点积。
令 A(i, j) 为矩阵 A 中第 i 行第 j 列的条目。 例如,A(3, 2) 是矩阵 A 中第 3 行第 2 列的条目。 假设 A、B 和 C 是矩阵,且 AB = C。C 的条目的计算如下:
C(i, j) = (A 的 i 行) • (B 的 j 列)
下图显示了矩阵乘法的几个示例。
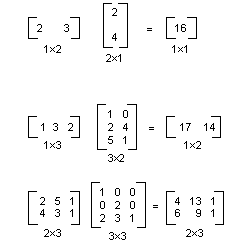
如果将平面中的点视为 1×2 矩阵,则可以通过将其乘以 2×2 矩阵来变换该点。 下图显示了应用于点 (2, 1) 的几个变换。
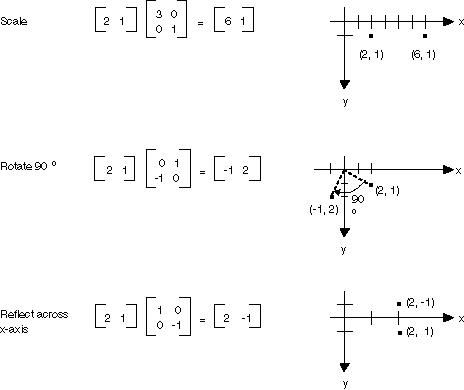
上图中显示的所有变换都是线性变换。 某些其他变换(例如平移)不是线性的,不能表示为与 2×2 矩阵相乘。 假设要从点 (2, 1) 开始,将其旋转 90 度,沿 x 方向平移 3 个单位,并沿 y 方向平移 4 个单位。 可以通过使用矩阵乘法和矩阵加法来实现此目的。
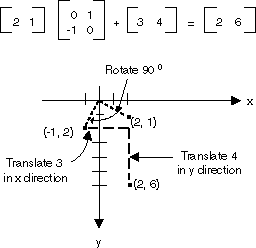
线性变换(与 2×2 矩阵相乘)后跟平移(与 1×2 矩阵相加)称为仿射变换。 将仿射变换存储在一对矩阵(一个用于线性部分,一个用于平移)中的另一种方法是将整个变换存储在 3×3 矩阵中。 为了实现此目的,必须将平面中的一个点存储在一个具有虚拟第三坐标的 1×3 矩阵中。 通常的方法是使所有第 3 个坐标等于 1。 例如,点 (2, 1) 由矩阵 [2 1 1] 表示。 下图显示了一个仿射变换(旋转 90 度;沿 x 方向平移 3 个单位,沿 y 方向平移 4 个单位),表示为与一个 3×3 矩阵相乘。
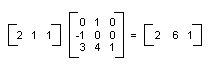
在前面的示例中,点 (2, 1) 映射到点 (2, 6)。 请注意,3×3 矩阵的第三列包含数字 0、0、1。 对于仿射变换的 3×3 矩阵来说,始终如此。 重要的数字是 1 列和 2 列中的六个数字。 矩阵左上角的 2×2 部分表示变换的线性部分,第 3 行的前两个条目表示平移。
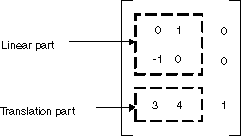
在 GDI+ 中,可以将仿射变换存储在 Matrix 对象中。 因为表示仿射变换的矩阵的第三列始终为 (0, 0, 1),所以在构造 Matrix 对象时仅指定前两列中的六个数字。 语句 Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) 构造了上图所示的矩阵。
复合变换
复合变换是一个接一个的一系列变换。 考虑以下列表中的矩阵和变换:
| Matrix | 转换 |
|---|---|
| 矩阵 A | 旋转 90 度 |
| 矩阵 B | 在 x 方向上缩放 2 倍 |
| 矩阵 C | 在 y 方向平移 3 个单位 |
如果我们从点 (2, 1) 开始 - 由矩阵 [2 1 1] 表示 - 然后依次乘以 A、B、C,点 (2, 1) 将按照所列的顺序进行三次变换。
[2 1 1]ABC = [-2 5 1]
与其将复合变换的三个部分存储在三个单独的矩阵中,不如将 A、B 和 C 相乘以得到一个 3×3 矩阵来存储整个复合变换。 假设 ABC = D。那么一个点乘以 D 得到的结果与一个点依次乘以 A、B、C 的结果相同。
[2 1 1]D = [-2 5 1]
下图显示了矩阵 A、B、C 和 D。
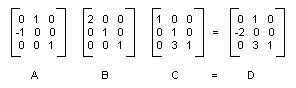
复合变换的矩阵可以通过乘以单个变换矩阵来形成,这一事实意味着任何顺序的仿射变换都可以存储在单个 Matrix 对象中。
注意
复合变换的顺序很重要。 一般来说,旋转、缩放、平移与缩放、旋转、平移是不同的。 同样,矩阵乘法的顺序也很重要。 一般来说,ABC 与 BAC 不同。
Matrix 类提供了几种构建复合变换的方法:Multiply、Rotate、RotateAt、Scale、Shear 和 Translate。 以下示例创建复合变换矩阵,该矩阵首先旋转 30 度,然后在 y 方向上缩放 2 倍,然后在 x 方向上平移 5 个单位:
Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)
下图显示了该矩阵。

另请参阅
反馈
即将发布:在整个 2024 年,我们将逐步淘汰作为内容反馈机制的“GitHub 问题”,并将其取代为新的反馈系统。 有关详细信息,请参阅:https://aka.ms/ContentUserFeedback。
提交和查看相关反馈
