Tutorial: Explore quantum entanglement with Q#
This tutorial shows you how to write a Q# program that manipulates and measures qubits and demonstrates the effects of superposition and entanglement. You prepare two qubits in a specific quantum state, learn how to operate on qubits with Q# to change their state, and demonstrate the effects of superposition and entanglement. You build your Q# program piece-by-piece to introduce qubit states, operations, and measurements.
Note
The Microsoft Quantum Development Kit (Classic QDK) will no longer be supported after June 30, 2024. If you are an existing QDK developer, we recommend that you transition to the new Azure Quantum Development Kit (Modern QDK) to continue developing quantum solutions. For more information, see Migrate your Q# code to the Modern QDK.
Here are some key concepts to understand before you begin:
- Where classical bits hold a single binary value such as a 0 or 1, the state of a qubit can be in a superposition of two quantum states, 0 and 1. Each possible quantum state has an associated probability amplitude.
- The act of measuring a qubit produces a binary result with a certain probability, and changes the state of the qubit out of superposition.
- Multiple qubits can be entangled such that they can't be described independently from each other. That is, whatever happens to one qubit in an entangled pair also happens to the other qubit.
In this tutorial, you'll learn how to:
- Create Q# operations to initialize a qubit to a desired state.
- Put a qubit in superposition.
- Entangle a pair of qubits.
- Measure a qubit and observe the results.
Tip
If you want to accelerate your quantum computing journey, check out Code with Azure Quantum, a unique feature of the Azure Quantum website. Here, you can run built-in Q# samples or your own Q# programs, generate new Q# code from your prompts, open and run your code in VS Code for the Web with one click, and ask Copilot any questions about quantum computing.
Prerequisites
To run the code sample in the Copilot for Azure Quantum, you need:
- A Microsoft (MSA) email account.
For more information about the Copilot, see Explore Azure Quantum.
Initialize a qubit to a known state
The first step is to define a Q# operation that will initialize a qubit to a known state. This can be called to set a qubit to a classical state, meaning that, when measured, it either returns Zero 100% of the time or returns One 100% of the time. Measuring a qubit returns a Q# type Result, which can only have a value of Zero or One.
Open the Copilot for Azure Quantum and copy the following code into the code editor window. Don't click Run yet; you'll run the code later in the tutorial.
namespace Bell {
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Canon;
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
}
The code example introduces two standard operations, M and X, which transform the state of a qubit.
The SetQubitState operation:
- Takes two parameters: a type
Result, nameddesired, that represents the desired state for the qubit to be in (ZeroorOne), and a typeQubit. - Performs a measurement operation,
M, which measures the state of the qubit (ZeroorOne) and compares the result to the value specified indesired. - If the measurement does not match the compared value, it runs an
Xoperation, which flips the state of the qubit to where the probabilities of a measurement returningZeroandOneare reversed. This way,SetQubitStatealways puts the target qubit in the desired state.
Write a test operation to test the Bell state
Next, to demonstrate the effect of the SetQubitState operation, create another operation named TestBellState. This operation will allocate two qubits, call SetQubitState to set the first qubit to a known state, and then measure the qubits to see the results.
Copy the following code into the code editor window, below the SetQubitState operation.
operation TestBellState() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = One;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
set numOnesQ1 += 1;
}
if resultQ2 == One {
set numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
In the code, the count and initial variables are set to 1000 and One respectively. This initializes the first qubit to One and measures each qubit 1000 times.
The TestBellStateoperation:
- Sets variables for the counter and the initial qubit state.
- Calls the
usestatement to initialize two qubits. - Loops for
countiterations. For each loop, it- Calls
SetQubitStateto set a specifiedinitialvalue on the first qubit. - Calls
SetQubitStateagain to set the second qubit to aZerostate. - Uses the
Moperation to measure each qubit. - Stores the number of measurements for each qubit that return
One.
- Calls
- After the loop completes, it calls
SetQubitStateagain to reset the qubits to a known state (Zero) to allow others to allocate the qubits in a known state. This is required by theusestatement. - Finally, it uses the
Messagefunction to print results to the Copilot output windows before returning the results.
Run the code in the Copilot for Azure Quantum
Before moving on to the procedures for superposition and entanglement, you can test the code up to this point to see the initialization and measurement of the qubits.
In order to run the code as a standalone program, the Q# compiler in the Copilot needs to know where to start the program. This is done in the Q# file by adding an @EntryPoint() directly preceding the operation that you want to run first. For example, in this case is the TestBellState operation.
Note
@EntryPoint() is only required for standalone Q# programs. When running a Q# program in Jupyter Notebooks, or calling a Q# program from a Python host file, it isn't required and will throw an error if included.
Add the @EntryPoint() immediately before TestBellState operation and your Q# program up to this point should now look like this:
namespace Bell {
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Canon;
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
@EntryPoint()
operation TestBellState() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = One;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
set numOnesQ1 += 1;
}
if resultQ2 == One {
set numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
}
Copy and paste the complete code sample into the Copilot for Azure Quantum code window, set the slide for the number of shots to "1", and click Run. The results are displayed in the histogram and in the Results fields.
Q1 - Zeros: 0
Q1 - Ones: 1000
Q2 - Zeros: 1000
Q2 - Ones: 0
Because the qubits haven't been manipulated yet, they have retained their initial values: the first qubit returns One every time, and the second qubit returns Zero.
If you change the value of initial to Zero and run the program again, you should observe that the first qubit also returns Zero every time.
Q1 - Zeros: 1000
Q1 - Ones: 0
Q2 - Zeros: 1000
Q2 - Ones: 0
Put a qubit in superposition
Currently, the qubits in the program are all in a classical state, that is, they are either 1 or 0. You know this because the program initializes the qubits to a known state, and you haven't added any processes to manipulate them. Before entangling the qubits, you will put the first qubit into a superposition state, where a measurement of the qubit will return Zero ~50% of the time and One ~50% of the time. Conceptually, the qubit can be thought of as having an equal probability of measuring either Zero or One.
To put a qubit in superposition, Q# provides the H, or Hadamard, operation. Recall the X operation from the Initialize a qubit to a known state procedure earlier, which flipped a qubit from 0 to 1 (or vice versa); the H operation flips the qubit halfway into a state of equal probabilities of Zero or One. When measured, a qubit in superposition should return roughly an equal number of Zero and One results.
Modify the code in the TestBellState operation by resetting the initial value to One and inserting a line for the H operation:
for test in 1..count {
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
H(q1); // Add the H operation after initialization and before measurement
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
...
Now when you run the program, you can see the results of the first qubit in superposition.
Q1 - Zeros: 523 // results will vary
Q1 - Ones: 477
Q2 - Zeros: 1000
Q2 - Ones: 0
Every time you run the program, the results for the first qubit will vary slightly, but will be close to 50% One and 50% Zero, while the results for the second qubit will remain Zero all the time.
Q1 - Zeros: 510
Q1 - Ones: 490
Q2 - Zeros: 1000
Q2 - Ones: 0
Initializing the first qubit to Zero returns similar results.
Q1 - Zeros: 504
Q1 - Ones: 496
Q2 - Zeros: 1000
Q2 - Ones: 0
Note
By moving the slider in the Copilot for Azure Quantum and increasing the number of shots, you can see how the superposition results vary slightly over the distribution of the shots.
Entangle two qubits
As mentioned earlier, entangled qubits are connected such that they cannot be described independently from each other. That is, whatever operation happens to one qubit, also happens to the entangled qubit. This allows you to know the resulting state of one qubit without measuring it, just by measuring the state of the other qubit. (This example uses two qubits; however, it is also possible to entangle three or more qubits).
To enable entanglement, Q# provides the CNOT operation, which stands for Controlled-NOT. The result of running this operation on two qubits is to flip the second qubit if the first qubit is One.
Add the CNOT operation to your program immediately after the H operation. Your full program should look like this:
namespace Bell {
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Canon;
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
@EntryPoint()
operation TestBellState() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = Zero;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
H(q1);
CNOT(q1, q2); // Add the CNOT operation after the H operation
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
set numOnesQ1 += 1;
}
if resultQ2 == One {
set numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
}
Now when you run the program you should see something like:
Q1 - Zeros: 502 // results will vary
Q1 - Ones: 498
Q2 - Zeros: 502
Q2 - Ones: 498
Notice that the statistics for the first qubit haven't changed (there is still a ~50/50 chance of a Zero or a One after measurement), but the measurement results for the second qubit are always the same as the measurement of the first qubit, no matter how many times you run the program. The CNOT operation has entangled the two qubits, so that whatever happens to one of them, happens to the other.
Prerequisites
To develop and run the code sample in your local development environment:
- The latest version of Visual Studio Code or open VS Code on the Web.
- The latest version of the Azure Quantum Development Kit extension. For installation details, see Installing the Modern QDK on VS Code.
Create a new Q# file
- Open Visual Studio Code and select File > New Text File to create a new file.
- Save the file as
CreateBellStates.qs. This file will contain the Q# code for your program.
Initialize a qubit to a known state
The first step is to define a Q# operation that will initialize a qubit to a known state. This can be called to set a qubit to a classical state, meaning it either returns Zero 100% of the time or returns One 100% of the time. Zero and One are Q# values that represent the only two possible results of a measurement of a qubit.
Open CreateBellStates.qs and copy the following code:
namespace Bell {
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Canon;
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
}
The code example introduces two standard operations, M and X, which transform the state of a qubit.
The SetQubitState operation:
- Takes two parameters: a type
Result, nameddesired, that represents the desired state for the qubit to be in (ZeroorOne), and a typeQubit. - Performs a measurement operation,
M, which measures the state of the qubit (ZeroorOne) and compares the result to the value specified indesired. - If the measurement does not match the compared value, it runs an
Xoperation, which flips the state of the qubit to where the probabilities of a measurement returningZeroandOneare reversed. This way,SetQubitStatealways puts the target qubit in the desired state.
Write a test operation to test the Bell state
Next, to demonstrate the effect of the SetQubitState operation, create another operation named TestBellState. This operation will allocate two qubits, call SetQubitState to set the first qubit to a known state, and then measure the qubits to see the results.
Add the following operation to your CreateBellStates.qs file after the SetQubitState operation:
operation TestBellState() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = One;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
set numOnesQ1 += 1;
}
if resultQ2 == One {
set numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
In the code, the count and initial variables are set to 1000 and One respectively. This initializes the first qubit to One and measures each qubit 1000 times.
The TestBellStateoperation:
- Takes two parameters:
count, the number of times to run a measurement, andinitial, the desired state to initialize the qubit. - Calls the
usestatement to initialize two qubits. - Loops for
countiterations. For each loop, it- Calls
SetQubitStateto set a specifiedinitialvalue on the first qubit. - Calls
SetQubitStateagain to set the second qubit to aZerostate. - Uses the
Moperation to measure each qubit. - Stores the number of measurements for each qubit that return
One.
- Calls
- After the loop completes, it calls
SetQubitStateagain to reset the qubits to a known state (Zero) to allow others to allocate the qubits in a known state. This is required by theusestatement. - Finally, it uses the
Messagefunction to print a message to the console before returning the results.
Run the code
Before moving on to the procedures for superposition and entanglement, test the code up to this point to see the initialization and measurement of the qubits.
This is done in the Q# file by adding an @EntryPoint() directly preceding the operation that you want to run. For example, in this case is the TestBellState operation.
Note
@EntryPoint() is only required for standalone Q# programs. When running a Q# program in Jupyter Notebooks, or calling a Q# program from a Python host file, it isn't required and will throw an error if included.
Your
CreateBellStates.qsfile should now look like this:namespace Bell { open Microsoft.Quantum.Intrinsic; open Microsoft.Quantum.Canon; operation SetQubitState(desired : Result, target : Qubit) : Unit { if desired != M(target) { X(target); } } @EntryPoint() operation TestBellState() : (Int, Int, Int, Int) { mutable numOnesQ1 = 0; mutable numOnesQ2 = 0; let count = 1000; let initial = One; // allocate the qubits use (q1, q2) = (Qubit(), Qubit()); for test in 1..count { SetQubitState(initial, q1); SetQubitState(Zero, q2); // measure each qubit let resultQ1 = M(q1); let resultQ2 = M(q2); // Count the number of 'Ones' returned: if resultQ1 == One { set numOnesQ1 += 1; } if resultQ2 == One { set numOnesQ2 += 1; } } // reset the qubits SetQubitState(Zero, q1); SetQubitState(Zero, q2); // Display the times that |0> is returned, and times that |1> is returned Message($"Q1 - Zeros: {count - numOnesQ1}"); Message($"Q1 - Ones: {numOnesQ1}"); Message($"Q2 - Zeros: {count - numOnesQ2}"); Message($"Q2 - Ones: {numOnesQ2}"); return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 ); } }Before running the program, you need to set the target profile to Unrestricted. Select View -> Command Palette, search for QIR, select Q#: Set the Azure Quantum QIR target profile, and then select Q#: unrestricted.
Note
If the target profile isn't set to Unrestricted, you will get an error when you run the program.
To run the program, select Run Q# File from the play icon drop-down in the top-right, click on Run from the list of commands below
@EntryPoint(), or press Ctrl+F5. The program runs the operation or function marked with the@EntryPoint()attribute on the default simulator.Your output appear in the debug console.
Q1 - Zeros: 0 Q1 - Ones: 1000 Q2 - Zeros: 1000 Q2 - Ones: 0Because the qubits haven't been manipulated yet, they have retained their initial values: the first qubit returns
Oneevery time, and the second qubit returnsZero.If you change the value of
initialtoZeroand run the program again, you should observe that the first qubit also returnsZeroevery time.Q1 - Zeros: 1000 Q1 - Ones: 0 Q2 - Zeros: 1000 Q2 - Ones: 0
Tip
Recall to save your file every time you introduce a change to the code before running it again.
Put a qubit in superposition
Currently, the qubits in the program are all in a classical state, that is, they are either 1 or 0. You know this because the program initializes the qubits to a known state, and you haven't added any processes to manipulate them. Before entangling the qubits, you will put the first qubit into a superposition state, where a measurement of the qubit will return Zero 50% of the time and One 50% of the time. Conceptually, the qubit can be thought of as halfway between the Zero and One.
To put a qubit in superposition, Q# provides the H, or Hadamard, operation. Recall the X operation from the Initialize a qubit to a known state procedure earlier, which flipped a qubit from Zero to One (or vice versa); the H operation flips the qubit halfway into a state of equal probabilities of Zero or One. When measured, a qubit in superposition should return roughly an equal number of Zero and One results.
Modify the code in the
TestBellStateoperation to include theHoperation:for test in 1..count { use (q1, q2) = (Qubit(), Qubit()); for test in 1..count { SetQubitState(initial, q1); SetQubitState(Zero, q2); H(q1); // Add the H operation after initialization and before measurement // measure each qubit let resultQ1 = M(q1); let resultQ2 = M(q2); ...Now when you run the program, you can see the results of the first qubit in superposition:
Q1 - Zeros: 523 // results will vary Q1 - Ones: 477 Q2 - Zeros: 1000 Q2 - Ones: 0Every time you run the program, the results for the first qubit will vary slightly, but will be close to 50%
Oneand 50%Zero, while the results for the second qubit will remainZeroall the time.Q1 - Zeros: 510 Q1 - Ones: 490 Q2 - Zeros: 1000 Q2 - Ones: 0Initializing the first qubit to
Zeroreturns similar results.Q1 - Zeros: 504 Q1 - Ones: 496 Q2 - Zeros: 1000 Q2 - Ones: 0
Entangle two qubits
As mentioned earlier, entangled qubits are connected such that they cannot be described independently from each other. That is, whatever operation happens to one qubit, also happens to the entangled qubit. This allows you to know the resulting state of one qubit without measuring it, just by measuring the state of the other qubit. (This example uses two qubits; however, it is also possible to entangle three or more qubits).
To enable entanglement, Q# provides the CNOT operation, which stands for Controlled-NOT. The result of running this operation on two qubits is to flip the second qubit if the first qubit is One.
Add the
CNOToperation to your program immediately after theHoperation. Your full program should look like this:namespace Bell { open Microsoft.Quantum.Intrinsic; open Microsoft.Quantum.Canon; operation SetQubitState(desired : Result, target : Qubit) : Unit { if desired != M(target) { X(target); } } @EntryPoint() operation TestBellState() : (Int, Int, Int, Int) { mutable numOnesQ1 = 0; mutable numOnesQ2 = 0; let count = 1000; let initial = One; // allocate the qubits use (q1, q2) = (Qubit(), Qubit()); for test in 1..count { SetQubitState(initial, q1); SetQubitState(Zero, q2); H(q1); CNOT(q1, q2); // Add the CNOT operation after the H operation // measure each qubit let resultQ1 = M(q1); let resultQ2 = M(q2); // Count the number of 'Ones' returned: if resultQ1 == One { set numOnesQ1 += 1; } if resultQ2 == One { set numOnesQ2 += 1; } } // reset the qubits SetQubitState(Zero, q1); SetQubitState(Zero, q2); // Display the times that |0> is returned, and times that |1> is returned Message($"Q1 - Zeros: {count - numOnesQ1}"); Message($"Q1 - Ones: {numOnesQ1}"); Message($"Q2 - Zeros: {count - numOnesQ2}"); Message($"Q2 - Ones: {numOnesQ2}"); return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 ); } }Q1 - Zeros: 502 Q1 - Ones: 498 // results will vary Q2 - Zeros: 502 Q2 - Ones: 498
The statistics for the first qubit haven't changed (a 50/50 chance of a Zero or a One after measurement), but the measurement results for the second qubit are always the same as the measurement of the first qubit. The CNOT operation has entangled the two qubits, so that whatever happens to one of them, happens to the other.
Plot the frequency histogram
Let's visualize the distribution of results obtained from running the quantum program multiple times. The frequency histogram helps visualize the probability distribution of these outcomes.
Select View -> Command Palette, or press Ctrl+Shift+P, and type “histogram” which should bring up the Q#: Run file and show histogram option. You can also click on Histogram from the list of commands below
@EntryPoint(). Select this option to open the Q# histogram window.Enter a number of shots to execute the program, for example, 100 shots, and press Enter. The histogram will display in the Q# histogram window.
Each bar in the histogram corresponds to a possible outcome, and its height represents the number of times that outcome is observed. In this case, there are 50 different unique results. Note that for each outcome the measurement results for the first and the second qubit are always the same.
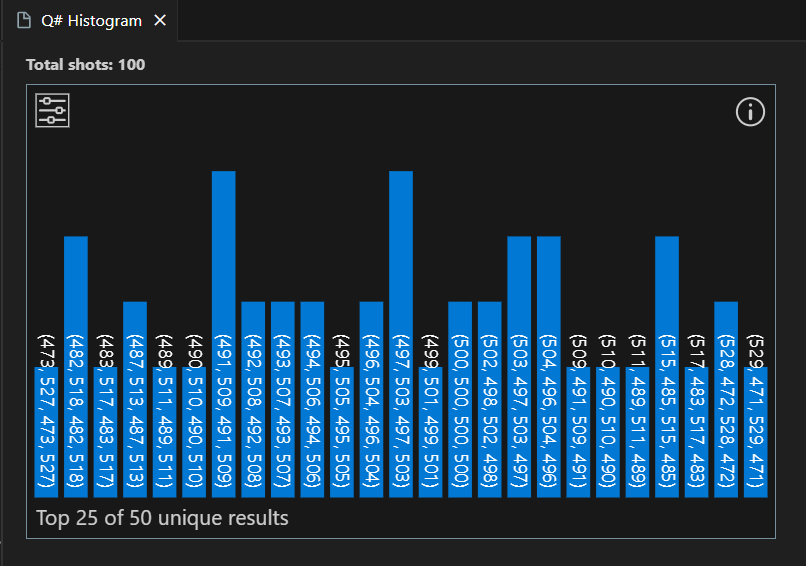
Tip
You can zoom the histogram using the mouse scroll wheel or a trackpad gesture. When zoomed in, you can pan the chart by pressing 'Alt' while scrolling.
Click on a bar to display the percentage of that outcome.
Click the top-left settings icon to display options. You can display top 10 results, top 25 results, or all results. You can also sort the results from high to low, or low to high.
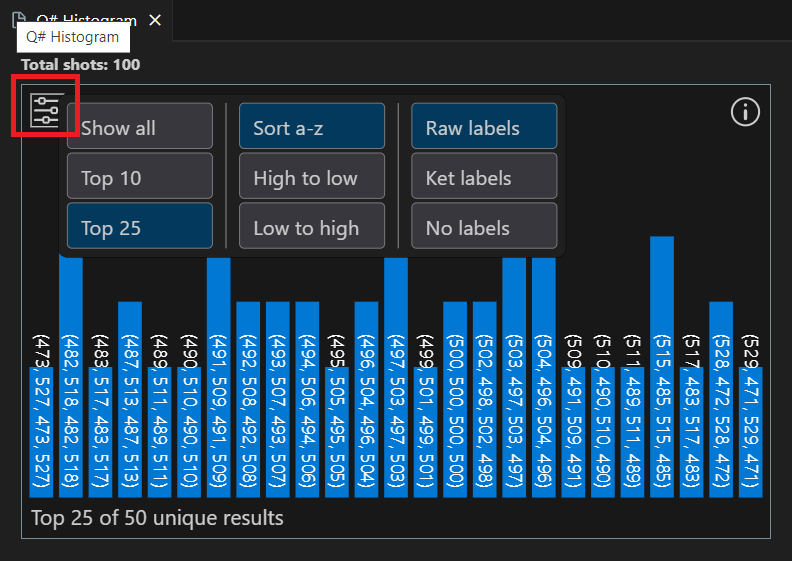
Next steps
Explore other Q# tutorials:
- Quantum random number generator shows how to write a Q# program that generates random numbers out of qubits in superposition.
- Grover's search algorithm shows how to write a Q# program that uses Grover's search algorithm.
- Quantum Fourier Transform explores how to write a Q# program that directly addresses specific qubits.
- The Quantum Katas are self-paced tutorials and programming exercises aimed at teaching the elements of quantum computing and Q# programming at the same time.
Feedback
Coming soon: Throughout 2024 we will be phasing out GitHub Issues as the feedback mechanism for content and replacing it with a new feedback system. For more information see: https://aka.ms/ContentUserFeedback.
Submit and view feedback for