Tutorial: Implement the Quantum Fourier Transform in Q#
Note
The Microsoft Quantum Development Kit (Classic QDK) will no longer be supported after June 30, 2024. If you are an existing QDK developer, we recommend that you transition to the new Azure Quantum Development Kit (Modern QDK) to continue developing quantum solutions. For more information, see Migrate your Q# code to the Modern QDK.
This tutorial shows you how to write and simulate a basic quantum program that operates on individual qubits.
Although Q# was primarily created as a high-level programming language for large-scale quantum programs, it can also be used to explore the lower level of quantum programming, that is, directly addressing specific qubits. Specifically, this tutorial takes a closer look at the Quantum Fourier Transform (QFT), a subroutine that is integral to many larger quantum algorithms.
In this tutorial, you'll learn how to:
- Define quantum operations in Q#.
- Write the Quantum Fourier Transform circuit
- Simulate a quantum operation from qubit allocation to measurement output.
- Observe how the quantum system's simulated wavefunction evolves throughout the operation.
Note
This lower level view of quantum information processing is often described in terms of quantum circuits, which represent the sequential application of gates, or operations, to specific qubits of a system. Thus, the single- and multi-qubit operations you sequentially apply can be readily represented in circuit diagrams. For example, the full three-qubit quantum Fourier transform used in this tutorial has the following representation as a circuit:
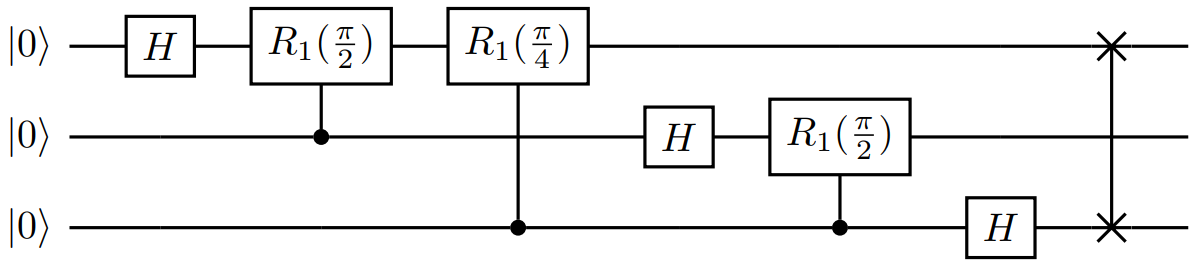
Tip
If you want to accelerate your quantum computing journey, check out Code with Azure Quantum, a unique feature of the Azure Quantum website. Here, you can run built-in Q# samples or your own Q# programs, generate new Q# code from your prompts, open and run your code in VS Code for the Web with one click, and ask Copilot any questions about quantum computing.
Prerequisites
The latest version of Visual Studio Code or open VS Code on the Web.
The latest version of the Azure Quantum Development Kit extension. For installation details, see Installing the Modern QDK on VS Code.
If you want to use Jupyter Notebooks, you also need to install Python, and Jupyter extensions, and the latest
qsharpPython package. To do so, open a terminal and run the following command:$ pip install --upgrade qsharp
Create a new Q# file
- In VS Code, select File > New Text File
- Save the file as QFTcircuit.qs. This file will contain the Q# code for your program.
- Open QFTcircuit.qs.
Write a QFT circuit in Q#
The first part of this tutorial consists of defining the Q# operation Perform3qubitQFT, which performs the quantum Fourier transform on three qubits. The DumpMachine function is used to observe how the simulated wavefunction of the three-qubit system evolves across the operation. In the second part of the tutorial, you will add measurement functionality and compare the pre- and post-measurement states of the qubits.
You will build the operation step by step. Copy and paste the code in the following sections into the QFTcircuit.qs file.
You can view the full Q# code for this section as reference.
Namespaces to access other Q# operations
Inside your Q# file, define the namespace NamespaceQFT, which is accessed by the compiler.
For this operation to make use of existing Q# operations, open the relevant Microsoft.Quantum.* namespaces.
namespace NamespaceQFT {
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Diagnostics;
open Microsoft.Quantum.Math;
open Microsoft.Quantum.Arrays;
// operations go here
}
Define operations with arguments and returns
Next, define the Perform3qubitQFT operation:
operation Perform3qubitQFT() : Unit {
// do stuff
}
For now, the operation takes no arguments and returns a Unit object, which is analogous to returning void in C# or an empty tuple, Tuple[()], in Python.
Later, you will modify the operation to return an array of measurement results.
Allocate qubits
Within the Q# operation, allocate a register of three qubits with the use keyword. With use, the qubits are automatically allocated in the $\ket{0}$ state.
use qs = Qubit[3]; // allocate three qubits
Message("Initial state |000>:");
DumpMachine();
As in real quantum computations, Q# does not allow you to directly access qubit states. However, the DumpMachine operation prints the target machine's current state, so it can provide valuable insight for debugging and learning when used in conjunction with the full state simulator.
Apply single-qubit and controlled operations
Next, you apply the operations that comprise the Perform3qubitQFT operation itself. Q# already contains these and many other basic quantum operations in the Microsoft.Quantum.Intrinsic namespace.
The first operation applied is the H (Hadamard) operation to the first qubit:
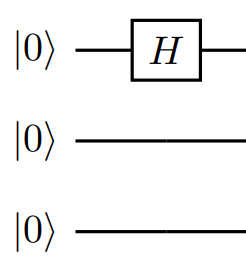
To apply an operation to a specific qubit from a register (for example, a single Qubit from an array Qubit[]), use standard index notation.
So, applying the H operation to the first qubit of the register qs takes the form:
H(qs[0]);
Besides applying the H operation to individual qubits, the QFT circuit consists primarily of controlled R1 rotations. A R1(θ, <qubit>) operation in general leaves the $\ket{0}$ component of the qubit unchanged while applying a rotation of $e^{i\theta}$ to the $\ket{1}$ component.
Q# makes it easy to condition the run of an operation upon one, or multiple, control qubits. In general, the call is prefaced with Controlled, and the operation arguments change as follows:
Op(<normal args>) $\to$ Controlled Op([<control qubits>], (<normal args>))
Note that the control qubit argument must be an array, even if it is for a single qubit.
The controlled operations in the QFT are the R1 operations that act on the first qubit (and controlled by the second and third qubits):
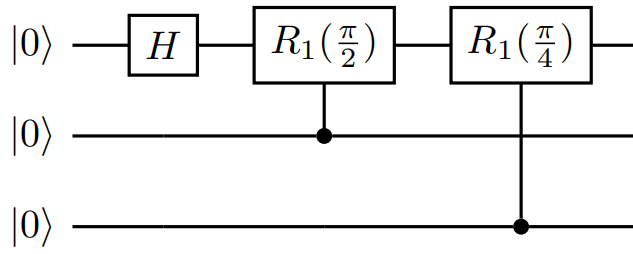
In your Q# file, call these operations with these statements:
Controlled R1([qs[1]], (PI()/2.0, qs[0]));
Controlled R1([qs[2]], (PI()/4.0, qs[0]));
The PI() function is used to define the rotations in terms of pi radians.
Apply SWAP operation
After applying the relevant H operations and controlled rotations to the second and third qubits, the circuit looks like this:
//second qubit:
H(qs[1]);
Controlled R1([qs[2]], (PI()/2.0, qs[1]));
//third qubit:
H(qs[2]);
Finally, you apply a SWAP operation to the first and third qubits to complete the circuit. This is necessary because the nature of the quantum Fourier transform outputs the qubits in reverse order, so the swaps allow for seamless integration of the subroutine into larger algorithms.
SWAP(qs[2], qs[0]);
Now you have finished writing the qubit-level operations of the quantum Fourier transform into your Q# operation:

Deallocate qubits
The last step is to call DumpMachine() again to see the post-operation state, and to deallocate the qubits. The qubits were in state $\ket{0}$ when you allocated them and need to be reset to their initial state using the ResetAll operation.
Requiring that all qubits be explicitly reset to $\ket{0}$ is a basic feature of Q#, as it allows other operations to know their state precisely when they begin using those same qubits (a scarce resource). Additionally, this assures that they are not entangled with any other qubits in the system. If the reset is not performed at the end of a use allocation block, a runtime error might be thrown.
Add the following lines to your Q# file:
Message("After:");
DumpMachine();
ResetAll(qs); // deallocate qubits
The complete QFT operation
The Q# program is completed. Your QFTcircuit.qs file should now look like this:
namespace NamespaceQFT {
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Diagnostics;
open Microsoft.Quantum.Math;
open Microsoft.Quantum.Arrays;
operation Perform3qubitQFT() : Unit {
use qs = Qubit[3]; // allocate three qubits
Message("Initial state |000>:");
DumpMachine();
//QFT:
//first qubit:
H(qs[0]);
Controlled R1([qs[1]], (PI()/2.0, qs[0]));
Controlled R1([qs[2]], (PI()/4.0, qs[0]));
//second qubit:
H(qs[1]);
Controlled R1([qs[2]], (PI()/2.0, qs[1]));
//third qubit:
H(qs[2]);
SWAP(qs[2], qs[0]);
Message("After:");
DumpMachine();
ResetAll(qs); // deallocate qubits
}
}
Run the QFT circuit
For now, the Perform3qubitQFT operation doesn't return any value - the operation returns Unit value. Later, you'll modify the operation to return an array of measurement results (Result[]).
When running a Q# program, you need to add an
EntryPointto the Q# file. This attribute tells the compiler that this operation is the entry point to the program. Add the following line to the top of your Q# file before thePerform3qubitQFToperation :@EntryPoint() operation Perform3qubitQFT() : Unit {Before running the program, you need to set the target profile to Unrestricted. Select View -> Command Palette, search for QIR, select Q#: Set the Azure Quantum QIR target profile, and then select Q#: unrestricted.
To run your program, select Run Q# File from the play icon drop-down in the top-right, or press Ctrl+F5. The program runs the operation or function marked with the
@EntryPoint()attribute on the default simulator.The
MessageandDumpMachineoutputs appear in the debug console.
Note
If the target profile is not set to Unrestricted, you will get an error when you run the program.
Understand the output of the QFT circuit
When called on the full-state simulator, DumpMachine() provides these multiple representations of the quantum state's wavefunction.
The possible states of an $n$-qubit system can be represented by $2^n$ computational basis states, each with a corresponding complex coefficient (an amplitude and a phase).
The computational basis states correspond to all the possible binary strings of length $n$, that is, all the possible combinations of qubit states $\ket{0}$ and $\ket{1}$, where each binary digit corresponds to an individual qubit.
The first row provides a comment with the IDs of the corresponding qubits in their significant order.
Qubit 2 being the "most significant" means that in the binary representation of basis state vector $\ket{i}$, the state of qubit 2 corresponds to the left-most digit.
For example, $\ket{6} = \ket{110}$ comprises qubits 2 and 1 both in $\ket{1}$ and qubit 0 in $\ket{0}$.
The rest of the rows describe the probability amplitude of measuring the basis state vector $\ket{i}$ in both Cartesian and polar formats. Examining the first row for the input state $\ket{000}$:
|0>:This row corresponds to the0computational basis state (given that the initial state post-allocation was $\ket{000}$, this is expected to be the only state with probability amplitude at this point).1.000000 + 0.000000 i: The probability amplitude in Cartesian format.==: theequalsign separates both equivalent representations.********************: A graphical representation of the magnitude. The number of*is proportionate to the probability of measuring this state vector.[ 1.000000 ]: The numeric value of the magnitude.---: A graphical representation of the amplitude's phase.[ 0.0000 rad ]: The numeric value of the phase (in radians).
Both the magnitude and the phase are displayed with a graphical representation. The magnitude representation is straightforward: it shows a bar of * and the higher the probability, the longer the bar will be.
The displayed output illustrates that the programmed operations transformed the state from
$$ \ket{\psi}_{initial} = \ket{000} $$
to
$$ \begin{align} \ket{\psi}_{final} &= \frac{1}{\sqrt{8}} \left( \ket{000} + \ket{001} + \ket{010} + \ket{011} + \ket{100} + \ket{101} + \ket{110} + \ket{111} \right) \\ &= \frac{1}{\sqrt{2^n}}\sum_{j=0}^{2^n-1} \ket{j}, \end{align} $$
which is precisely the behavior of the three-qubit Fourier transform.
If you are curious about how other input states are affected, you are encouraged to experiment with applying other qubit operations before the transform.
Add measurements to the QFT circuit
The display from the DumpMachine function showed the results of the operation, but unfortunately, a cornerstone of quantum mechanics states that a real quantum system cannot have such a DumpMachine function.
Instead, the information is extracted through measurements, which in general not only fail to provide information on the full quantum state, but can also drastically alter the system itself.
There are many sorts of quantum measurements, but the example here focuses on the most basic: projective measurements on single qubits. Upon measurement in a given basis (for example, the computational basis $ { \ket{0}, \ket{1} } $), the qubit state is projected onto whichever basis state was measured, hence destroying any superposition between the two.
Modify the QFT operation
To implement measurements within a Q# program, use the M operation, which returns a Result type.
First, modify the Perform3QubitQFT operation to return an array of measurement results, Result[], instead of Unit.
operation Perform3QubitQFT() : Result[] {
Define and initialize Result[] array
Before allocating qubits, declare and bind a three-element array (one Result for each qubit):
mutable resultArray = [Zero, size = 3];
The mutable keyword prefacing resultArray allows the variable to be modified later in the code, for example, when adding your measurement results.
Perform measurements in a for loop and add results to array
After the QFT transform operations, insert the following code:
for i in IndexRange(qs) {
set resultArray w/= i <- M(qs[i]);
}
The IndexRange function called on an array (for example, the array of qubits, qs) returns a range over the indices of the array.
Here, it is used in the for loop to sequentially measure each qubit using the M(qs[i]) statement.
Each measured Result type (either Zero or One) is then added to the corresponding index position in resultArray with an update-and-reassign statement.
Note
The syntax of this statement is unique to Q#, but corresponds to the similar variable reassignment resultArray[i] <- M(qs[i]) seen in other languages such as F# and R.
The keyword set is always used to reassign variables bound using mutable.
Return resultArray
With all three qubits measured and the results added to resultArray, you are safe to reset and deallocate the qubits as before. To
return the measurements, insert:
return resultArray;
Run the QFT circuit with the measurements
Now change the placement of the DumpMachine functions to output the state before and after the measurements.
Your final Q# code should look like this:
namespace NamespaceQFT {
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Diagnostics;
open Microsoft.Quantum.Math;
open Microsoft.Quantum.Arrays;
operation Perform3QubitQFT() : Result[] {
mutable resultArray = [Zero, size = 3];
use qs = Qubit[3];
//QFT:
//first qubit:
H(qs[0]);
Controlled R1([qs[1]], (PI()/2.0, qs[0]));
Controlled R1([qs[2]], (PI()/4.0, qs[0]));
//second qubit:
H(qs[1]);
Controlled R1([qs[2]], (PI()/2.0, qs[1]));
//third qubit:
H(qs[2]);
SWAP(qs[2], qs[0]);
Message("Before measurement: ");
DumpMachine();
for i in IndexRange(qs) {
set resultArray w/= i <- M(qs[i]);
}
Message("After measurement: ");
DumpMachine();
ResetAll(qs);
Message("Post-QFT measurement results [qubit0, qubit1, qubit2]: ");
return resultArray;
}
}
Tip
Recall to save your file every time you introduce a change to the code before running it again.
Add an
EntryPointbefore thePerform3qubitQFToperation :@EntryPoint() operation Perform3qubitQFT() : Unit {Set the target profile to Unrestricted. Click on the QIR: Base button in the bottom of the VS Code window and select Unrestricted from the dropdown menu. If the target profile is not set to Unrestricted, you will get an error when you run the program.
To run your program, select Run Q# file from the play icon drop-down in the top-right, or press Ctrl+5. The program runs the operation or function marked with the
@EntryPoint()attribute on the default simulator.The
MessageandDumpMachineoutputs appear in the debug console.
Your output should look similar to the output:
Before measurement:
# wave function for qubits with ids (least to most significant): 0;1;2
|0>: 0.353553 + 0.000000 i == *** [ 0.125000 ] --- [ 0.00000 rad ]
|1>: 0.353553 + 0.000000 i == *** [ 0.125000 ] --- [ 0.00000 rad ]
|2>: 0.353553 + 0.000000 i == *** [ 0.125000 ] --- [ 0.00000 rad ]
|3>: 0.353553 + 0.000000 i == *** [ 0.125000 ] --- [ 0.00000 rad ]
|4>: 0.353553 + 0.000000 i == *** [ 0.125000 ] --- [ 0.00000 rad ]
|5>: 0.353553 + 0.000000 i == *** [ 0.125000 ] --- [ 0.00000 rad ]
|6>: 0.353553 + 0.000000 i == *** [ 0.125000 ] --- [ 0.00000 rad ]
|7>: 0.353553 + 0.000000 i == *** [ 0.125000 ] --- [ 0.00000 rad ]
After measurement:
# wave function for qubits with ids (least to most significant): 0;1;2
|0>: 0.000000 + 0.000000 i == [ 0.000000 ]
|1>: 0.000000 + 0.000000 i == [ 0.000000 ]
|2>: 0.000000 + 0.000000 i == [ 0.000000 ]
|3>: 1.000000 + 0.000000 i == ******************** [ 1.000000 ] --- [ 0.00000 rad ]
|4>: 0.000000 + 0.000000 i == [ 0.000000 ]
|5>: 0.000000 + 0.000000 i == [ 0.000000 ]
|6>: 0.000000 + 0.000000 i == [ 0.000000 ]
|7>: 0.000000 + 0.000000 i == [ 0.000000 ]
Post-QFT measurement results [qubit0, qubit1, qubit2]:
[One,One,Zero]
This output illustrates a few different things:
- Comparing the returned result to the pre-measurement
DumpMachine, it clearly does not illustrate the post-QFT superposition over basis states. A measurement only returns a single basis state, with a probability determined by the amplitude of that state in the system's wavefunction. - From the post-measurement
DumpMachine, you see that measurement changes the state itself, projecting it from the initial superposition over basis states to the single basis state that corresponds to the measured value.
If you repeat this operation many times, you will see the result statistics begin to illustrate the equally weighted superposition of the post-QFT state that gives rise to a random result on each shot. However, besides being inefficient and still imperfect, this would nevertheless only reproduce the relative amplitudes of the basis states, not the relative phases between them. The latter is not an issue in this example, but you would see relative phases appear if given a more complex input to the QFT than $\ket{000}$.
Use the Q# operations to simplify the QFT circuit
As mentioned in the introduction, much of Q#'s power rests in the fact that it allows you to abstract-away the worries of dealing with individual qubits.
Indeed, if you want to develop full-scale, applicable quantum programs, worrying about whether an H operation goes before or after a particular rotation would only slow you down.
The Q# namespace Microsoft.Quantum.Canon contains the ApplyQFT operation, which you can use and apply for any number of qubits.
To access the
ApplyQFToperation, addopenstatement for theMicrosoft.Quantum.Canonnamespace at the beginning of the Q# file:open Microsoft.Quantum.Canon;Replace everything from the first
Hto theSWAPreplaced by:ApplyQFT(qs);Run the Q# program again and notice that the output is the same as before.
To see the real benefit of using Q# operations, change the number of qubits to something other than
3:
mutable resultArray = [Zero, size = 4];
use qs = Qubit[4];
//...
You can thus apply the proper QFT for any given number of qubits, without having to worry about the mess of new H operations and rotations on each qubit.
Next steps
Explore other Q# tutorials:
- Quantum random number generator shows how to write a Q# program that generates random numbers out of qubits in superposition.
- Grover's search algorithm shows how to write a Q# program that uses Grover's search algorithm.
- Quantum entanglement shows how to write a Q# program that manipulates and measures qubits and demonstrates the effects of superposition and entanglement.
- The Quantum Katas are self-paced tutorials and programming exercises aimed at teaching the elements of quantum computing and Q# programming at the same time.
Feedback
Coming soon: Throughout 2024 we will be phasing out GitHub Issues as the feedback mechanism for content and replacing it with a new feedback system. For more information see: https://aka.ms/ContentUserFeedback.
Submit and view feedback for