TrueType hinting tutorial - Basic hinting philosophies and TrueType instructions
In this section we will look at goals of hinting, hinting with TrueType and individual glyph hinting. This section contains some of what is stored in the TrueType glyph table ('glyf').
The ultimate goal of hinting is to best represent the font at all the resolutions at which it will be displayed. PCs use several different resolutions and aspect ratios. The most common are the VGA at 96 dots per inch, SVGA at 120 dpi and the Macintosh at 72 dpi. All these devices have a 1:1 aspect ratio. When a font is hinted, the type engineer determines the lowest pixel per em size to which they will hint and retain satisfactory results. Commonly the lowest ppem size hinted is 9. This is the equivalent of 7 point on a VGA screen, 5.5 point on an SVGA and 9 point on a Macintosh. Some PC screens and some printers have a non square aspect ratio. Microsoft Core fonts have code in the preprogram to check for the current aspect ratio.
Some of our goals will already have been solved in the 'prep' program controlling global issues. In preparation we've looked at whether all fonts can use the same height values in the 'cvt' for the tops of the uppercase, lowercase, xheight, ascenders, etc, whether the overshoots are the same and when they turn on.
The first example we'll look at is the hinting of an italic uppercase 'O'.
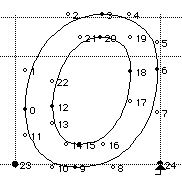
Figure 2a. TrueType outline of an UC O.
High level hinting strategy for hinting the uppercase O in figure 2
- Control the top and bottom to be consistent with other uppercase glyphs.
- Control the top curve and bottom curve to be the same and consistent with other uc curves.
- Control the left curve and right curve to be the same and consistent with other uc curves.
- Fix all points not instructed by moving them to smooth the outline.
A lower level hinting strategy for figure 2
In writing the code for hinting, it is more efficient to hint in one direction fully before switching to the other direction. This is not a requirement in TrueType. I begin by controlling the Y (vertical) direction and the height. Then I process the X (horizontal) direction.
- Set the hinting direction to Y.
- Move pt 3 to the control value that corresponds to the "uc top round height" and round this to a grid line. (Distances and values when converted to pixels are usually in fractions of pixels. These fractions of pixels are converted into whole, half or specified fractions of pixels. Example: a distance is 1.4 pixels. When this distance is rounded to grid, it would equal 1 pixel.)
- Move pt 9 to the control value that corresponds to the "uc bottom round height" and round this to a grid line.
- Control the distance between pt3 and pt20 to a control value for "uc Y round" or its actual distance and round pt 20 to a grid boundary.
- Control the distance between pt9 and pt15 to a control value for "uc Y round" or its actual distance and round pt 15 to a grid boundary.
- Set the direction to X
- Put pt 0 on a grid boundary.
- Control the distance between pt0 and pt12 to a control value for "uc X round" or its actual distance and round pt 12 to a grid boundary.
- Put pt 6 on a grid boundary.
- Control the distance between pt6 and pt18 to a control value for "uc X round" or its actual distance and round pt 18 to a grid boundary.
- Interpolate all points that were untouched between points that were touched in the X and Y direction. (Moving points between two moved key points and keeping the relation the same as the original positions of all points.)
TrueType instructions for figure 2
Hinting instructions move key points on a glyph. When these key points are moved their X,Y coordinates are converted to pixels and fractions of pixels. When these pixel amounts are rounded by instructions they are dependent on the setting of the 'round_state' variable. The default setting is 'round to grid'. The other possible settings are: round to half grid, round to the closest grid or half grid, round up to grid, round down to grid, rounding off (don't round) and finally finer control of the round_state. The round_state setting in our example is 'round to grid'.
SVTCA[Y] /* set the hint direction to Y */
MIAP[R], 3,3 /* move pt 3 to the value of cvt 3 and rounding the value*/
MIAP[R], 9,9 /* move pt 9 to the value of cvt 9 and rounding the value*/
SRP0[], 3 /* set the current reference point to pt 3 */
MIRP[m>RBl], 20, 73 /* control the top round feature */
SRP0[], 9 /* set the current reference point to pt 9 */
MIRP[m>RBl], 15, 73 /* control the bottom round feature */
SVTCA[X] /*set the direction to X */
SRP0[], 23 /*hinting from the left sidebearing point */
MDRP[MRBl], 12, 69 /*controlling the left round distance */
SRP0[], 24 /*hinting from the right sidebearing point */
MDRP[MRBl], 18, 69 /* controlling the right round distance */
IUP[X] /* interpolating all unused points in the X direction */
IUP[Y] /* interpolating all unused points in the Y direction */
(Sidebearing: The distance from the leftmost portion of a glyph and its origin or the rightmost portion and the end of the glyph's advance width, which is the total space occupied by the glyph itself and its two sidebearings. )
Let's look at each line more specifically:
- SVTCA[Y]
Sets the hinting direction to the vertical or Y direction. Translated: Set the Vectors to Control Axis Y. Vectors are straight line segments. There are three vectors in the "graphic state": one called the 'projection vector', one called the 'freedom vector' and another called the 'dual projection vector' . The projection vector is how distances are measured. The freedom vector is the direction in which points are moved (X,Y or diagonal). The dual projection vector is used by some instructions for measuring between points from their original ungrid-fitted position. - MIAP[R], 3,3
Move Indirect Absolute Point. Moves point 3 to the value of CVT 3 and rounded. Indirect refers to the use of a CVT as opposed to directly using the actual coordinate distance. The direct method of rounding a point would be coded as: MDAP[R], 3 - MIAP[R], 9,9
Same as MIAP[R], 3,3 but uses point 9 and CVT 9. - SRP0[], 3
Set Reference Point Zero to point 3. Sets the current reference point to pt3. Later when we code an instruction with a 'relative' point it needs a 'reference' point. If pt 'b' is a relative point it is dependent on the position of pt 'a', a point of reference or "reference" point. - MIRP[m>RBl], 20, 73
Move Indirect Relative Point. Moves and rounds pt20. Outline point 20 is a relative point and is moving in relation to the reference point 3 which was set in the previous instruction SRP0. It is an Indirect point because we are using a cvt to control its distance. A MIRP instruction takes four arguments. The first three arguments are boolean values. Here we are using symbols that correspond to our TrueType editor.
The first argument can be set to make the MIRP point the next reference point, such as is done with the SRP0 instruction or it can not be set. This case 'm' represents it is not set.
The second argument can be set to keep the distance greater than or equal to the minimum distance or it can not keep the distance. Here since this is across a round stroke we want to maintain the distance so it is set here with a '>' symbol.
The third boolean argument does two things: rounds the distance to a grid boundary and looks at the 'cvt' cut-in limit set in by the 'prep' table. Or don't round the distance and don't look at the 'cvt' cut-in limit.
The last argument is for defining whether this distance is across a black feature, a white feature or a gray feature. An example of a black feature is across the stem of the uppercase 'I' in the X direction. An example of a white feature is across a counter (the white space) in an 'O' or from a sidebearing. A gray feature is when this hint crosses a black feature and a white feature.
- SRP0[], 9
Sets outline point 9 as the current reference point. - MIRP[m>RBl], 15, 73
Moves pt15 to a grid boundary. Controls the bottom round feature the same as we controlled the top. Uses the same 'cvt' 73 that corresponds to the uc Y Round cvt. - SVTCA[X]
Sets the direction to X. - SRP0[], 23
Sets pt23 as the current reference point. Point 23 and 24 are not points that are on the outline. They are called 'Phantom' points. These points are showing the left sidebearing and the advance width on the baseline. (A glyph's horizontal distance including the white space on either side.) The Phantom points can be controlled by instructions. Here we are hinting from these Phantom points inward to the glyph. We don't need to use an instruction to move the point since Phantom points are always on a grid boundary. - MDRP[M>RWh], 0
Move Direct Relative Point. Moves and rounds pt0. Similar to a MIRP but this instruction does not use a control value. Argument 1 ('M') is set so pt0 becomes the current reference point . The second argument is set not to maintain minimum distance. We're rounding the point and this is a white feature. Uses the actual distance from pt23 to pt0 when moving pt0. - MIRP[m>RBl], 12, 69
Moves pt12 to a grid boundary. Uses cvt 69 for uc X Round features and controls the left round of the glyph. The arguments are set the same as for the Y round features. - SRP0[], 24
Sets pt24 as the current reference point. We are starting to hint the right side of the glyph. Coming in from the Phantom point 24. - MDRP[M>RWh], 6
Moves pt6 to a grid boundary. Same hints as on the left side. We're moving point 6 by its actual distance from point 24 and not using a cvt value. By hinting in from the sidebearings we can preserve the relationship of the glyph and its sidebearings and preserve spacing. - MIRP[m>RBl], 18, 69
Moves pt18 to a grid boundary. Using the same cvt 69, for controlling the right X Round feature. - IUP[X]
Interpolate Unused Points. Smooths the outline by moving points in the X direction in relation to points which have been hinted in the X direction. - IUP[Y]
Smooths out the Y direction.